ЬтФПФкШн
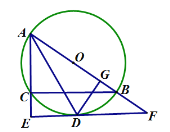
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН10cmЃЌBDЁЭACгкЕуDЃЌBDЃН8cmЃЎЕуMДгЕуAГіЗЂЃЌбиACЕФЗНЯђдШЫйдЫЖЏЃЌЭЌЪБжБЯпPQгЩЕуBГіЗЂЃЌбиBAЕФЗНЯђдШЫйдЫЖЏЃЌдЫЖЏЙ§ГЬжаЪМжеБЃГжPQЁЮACЃЌжБЯпPQНЛABгкЕуPЁЂНЛBCгкЕуQЁЂНЛBDгкЕуFЃЎСЌНгPMЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЁм5ЃЉЃЎЯпЖЮCMЕФГЄЖШМЧзїyМзЃЌЯпЖЮBPЕФГЄЖШМЧзїyввЃЌyМзКЭyввЙигкЪБМфtЕФКЏЪ§БфЛЏЧщПіШчЭМЫљЪОЃЎ
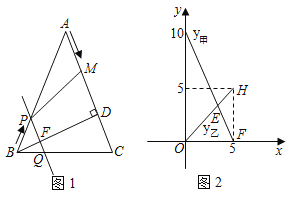
ЃЈ1ЃЉгЩЭМ2ПЩжЊЃЌЕуMЕФдЫЖЏЫйЖШЪЧУПУыЁЁ cmЃЛЕБtЃНЁЁ УыЪБЃЌЫФБпаЮPQCMЪЧЦНааЫФБпаЮЃПдкЭМ2жаЗДгГетвЛЧщПіЕФЕуЪЧЁЁ ЃЈВЂаДГіДЫЕуЕФзјБъЃЉЃЛ
ЃЈ2ЃЉЩшЫФБпаЮPQCMЕФУцЛ§ЮЊycm2ЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉСЌНгPCЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕуMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ![]() ЃЌEЃЈ
ЃЌEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ2ЃЉyЃН
ЃЉЃЛЃЈ2ЃЉyЃН![]() t2Љ8t+40ЃЛЃЈ3ЃЉДцдкЃЌtЃН
t2Љ8t+40ЃЛЃЈ3ЃЉДцдкЃЌtЃН![]() sЪБЃЌЕуMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃЎ
sЪБЃЌЕуMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШгЩЭМ2ХаЖЯГіЕуMЕФЫйЖШЮЊ2cm/sЃЌPQЕФдЫЖЏЫйЖШЮЊ1cm/sЃЌдйгЩЫФБпаЮPQCMЮЊЦНааЫФБпаЮЃЌИљОнЦНааЫФБпаЮЕФаджЪЕУЕНЖдБпЦНааЃЌНјЖјЕУЕНAP=AMЃЌСаГіЙигкtЕФЗНГЬЃЌЧѓГіЗНГЬЕФНтЕУЕНТњзуЬтвтtЕФжЕЃЛ
ЃЈ2ЃЉИљОнPQЁЮACПЩЕУЁїPBQЁзЁїABCЃЌИљОнЯрЫЦШ§НЧаЮЕФаЮзДБиШЛЯрЭЌПЩжЊЁїBPQвВЮЊЕШбќШ§НЧаЮЃЌМДBP=PQ=tЃЌдйгУКЌtЕФДњЪ§ЪНОЭПЩвдБэЪОГіBFЃЌНјЖјЕУЕНЬнаЮЕФИпPE=DF=8-tЃЌгжЕуMЕФдЫЖЏЫйЖШКЭЪБМфПЩжЊЕуMзпЙ§ЕФТЗГЬAM=2tЃЌЫљвдЬнаЮЕФЯТЕзCM=10-2tЃЎзюКѓИљОнЬнаЮЕФУцЛ§ЙЋЪНМДПЩЕУЕНyгыtЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉМйЩшДцдкЃЌдђИљОнДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮСНЖЫЕуЕФОрРыЯрЕШМДПЩЕУЕНMP=MCЃЌЙ§ЕуMзїMHДЙжБABЃЌгЩвЛЖдЙЋЙВНЧЕФЯрЕШКЭвЛЖджБНЧЕФЯрЕШМДПЩЕУЕНЁїAHMЁзЁїADBЃЌгЩЯрЫЦЕУЕНЖдгІБпГЩБШР§НјЖјгУКЌtЕФДњЪ§ЪНБэЪОГіAHКЭHMЕФГЄЃЌдйгЩAPЕФГЄМѕAHЕФГЄБэЪОГіPHЕФГЄЃЌДгЖјдкжБНЧШ§НЧаЮPHMжаИљОнЙДЙЩЖЈРэБэЪОГіMPЕФЦНЗНЃЌдйгЩACЕФГЄМѕAMЕФГЄБэЪОГіMCЕФЦНЗНЃЌИљОнСНепЕФЯрЕШСаГіЙигкtЕФЗНГЬНјЖјЧѓГіtЕФжЕЃЎ
ЃЈ1ЃЉгЩЭМ2ЕУЃЌЕуMЕФдЫЖЏЫйЖШЮЊ2cm/sЃЌPQЕФдЫЖЏЫйЖШЮЊ1cm/sЃЌ
ЁпЫФБпаЮPQCMЪЧЦНааЫФБпаЮЃЌдђPMЁЮQCЃЌ
ЁрAPЃКABЃНAMЃКACЃЌ
ЁпABЃНACЃЌ
ЁрAPЃНAMЃЌМД10ЉtЃН2tЃЌ
НтЕУЃКtЃН![]() ЃЌ
ЃЌ
ЁрЕБtЃН![]() ЪБЃЌЫФБпаЮPQCMЪЧЦНааЫФБпаЮЃЌДЫЪБЃЌЭМ2жаЗДгГетвЛЧщПіЕФЕуЪЧEЃЈ
ЪБЃЌЫФБпаЮPQCMЪЧЦНааЫФБпаЮЃЌДЫЪБЃЌЭМ2жаЗДгГетвЛЧщПіЕФЕуЪЧEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЙЪД№АИЮЊЃК2ЃЌ![]() ЃЌEЃЈ
ЃЌEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ2ЃЉЁпPQЁЮACЃЌ
ЁрЁїPBQЁзЁїABCЃЌ
ЁрЁїPBQЮЊЕШбќШ§НЧаЮЃЌPQЃНPBЃНtЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]()
НтЕУЃКBFЃН![]() tЃЌ
tЃЌ
ЁрFDЃНBDЉBFЃН8Љ![]() tЃЌ
tЃЌ
гжЁпMCЃНACЉAMЃН10Љ2tЃЌ
ЁрyЃН![]() ЃЈPQ+MCЃЉFDЃН
ЃЈPQ+MCЃЉFDЃН![]() ЃЈt+10Љ2tЃЉЃЈ8Љ
ЃЈt+10Љ2tЃЉЃЈ8Љ![]() tЃЉЃН
tЃЉЃН![]() t2Љ8t+40ЃЎ
t2Љ8t+40ЃЎ
ЃЈ3ЃЉМйЩшДцдкФГвЛЪБПЬtЃЌЪЙЕУMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃЌдђMPЃНMCЃЌ
Й§MзїMHЁЭABЃЌНЛABгыHЃЌШчЭМЫљЪОЃК
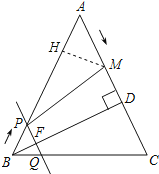
ЁпЁЯAЃНЁЯAЃЌЁЯAHMЃНЁЯADBЃН90ЁуЃЌ
ЁрЁїAHMЁзЁїADBЃЌ
Ёр![]()
гжЁпADЃН6ЃЌ
Ёр![]()
ЁрHMЃН![]() tЃЌAHЃН
tЃЌAHЃН![]() tЃЌ
tЃЌ
ЁрHPЃН10ЉtЉ![]() tЃН10Љ
tЃН10Љ![]() tЃЌ
tЃЌ
дкRtЁїHMPжаЃЌMP2ЃНЃЈ![]() tЃЉ2+ЃЈ10Љ
tЃЉ2+ЃЈ10Љ![]() tЃЉ2ЃН
tЃЉ2ЃН![]() t2Љ44t+100ЃЌ
t2Љ44t+100ЃЌ
гжЁпMC2ЃНЃЈ10Љ2tЃЉ2ЃН100Љ40t+4t2ЃЌ
ЁпMP2ЃНMC2ЃЌ
Ёр![]() t2Љ44t+100ЃН100Љ40t+4t2ЃЌ
t2Љ44t+100ЃН100Љ40t+4t2ЃЌ
НтЕУ t1ЃН![]() ЃЌt2ЃН0ЃЈЩсШЅЃЉЃЌ
ЃЌt2ЃН0ЃЈЩсШЅЃЉЃЌ
ЁрtЃН![]() sЪБЃЌЕуMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃЎ
sЪБЃЌЕуMдкЯпЖЮPCЕФДЙжБЦНЗжЯпЩЯЃЎ

 УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ
УїЬьНЬг§ПЮЪБЬибЕЯЕСаД№АИ еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ
еуНаТПЮГЬШ§ЮЌФПБъВтЦРПЮЪБЬибЕЯЕСаД№АИ жмжмЧхМьВтЯЕСаД№АИ
жмжмЧхМьВтЯЕСаД№АИ ЧсЧЩЖсЙкжмВтдТПМжБЭЈИпПМЯЕСаД№АИ
ЧсЧЩЖсЙкжмВтдТПМжБЭЈИпПМЯЕСаД№АИЁОЬтФПЁПЮвЪаФГаЃПЊеЙСЫвдЁАУЮЯыжаЙњЁБЮЊжїЬтЕФЩугАДѓШќЃЌвЊЧѓВЮШќбЇЩњУПШЫНЛвЛМўзїЦЗЃЎЯжНЋ
ДгжаЬєбЁЕФ50МўВЮШќзїЦЗЕФГЩМЈЃЈЕЅЮЛЃКЗжЃЉЭГМЦШчЯТЃК
ЕШМЖ | ГЩМЈЃЈгУmБэЪОЃЉ | ЦЕЪ§ | ЦЕТЪ |
A | 90Ём m Ём100 | x | 0.08 |
B | 80Ём m ЃМ90 | 34 | y |
C | m ЃМ80 | 12 | 0.24 |
КЯМЦ |
| 50 | 1 |
ЧыИљОнЩЯБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжа![]() ЕФжЕЮЊ_____________ЃЌ
ЕФжЕЮЊ_____________ЃЌ![]() ЕФжЕЮЊ______________ЃЛЃЈжБНгЬюаДНсЙћЃЉ
ЕФжЕЮЊ______________ЃЛЃЈжБНгЬюаДНсЙћЃЉ
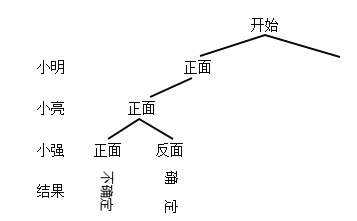
ЃЈ2ЃЉНЋБОДЮВЮШќзїЦЗЛёЕУAЕШМЖЕФбЇЩњвРДЮгУA1ЁЂA2ЁЂA3ЁЁБэЪОЃЎЯжИУаЃОіЖЈДгБОДЮВЮШќзїЦЗЛёЕУAЕШМЖЕФбЇЩњжаЃЌЫцЛњГщШЁСНУћбЇЩњЬИЬИЫћУЧЕФВЮШќЬхЛсЃЌдђЧЁКУГщЕНбЇЩњA1КЭA2ЕФИХТЪЮЊ____________ЃЎЃЈжБНгЬюаДНсЙћЃЉ
ЁОЬтФПЁПФГжжаЭКХЕФЮТПиЫЎЯфЕФЙЄзїЙ§ГЬЪЧЃКНгЭЈЕчдДКѓЃЌдкГѕЪМЮТЖШ20ЁцЯТМгШШЫЎЯфжаЕФЫЎЃЛЕБЫЎЮТДяЕНЩшЖЈЮТЖШ80ЁцЪБЃЌМгШШЭЃжЙЃЛДЫКѓЫЎЯфжаЕФЫЎЮТПЊЪМж№НЅЯТНЕЃЌЕБЯТНЕЕН20ЁцЪБЃЌдйДЮздЖЏМгШШЫЎЯфжаЕФЫЎжС80ЁцЪБЃЌМгШШЭЃжЙЃЛЕБЫЎЯфжаЕФЫЎЮТЯТНЕЕН20ЁцЪБЃЌдйДЮздЖЏМгШШЃЌЁЃЌАДеевдЩЯЗНЪНВЛЖЯбЛЗЃЎ
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдИУаЭКХЮТПиЫЎЯфжаЕФЫЎЮТЫцЪБМфБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЗЂЯжЫЎЮТyЪЧЪБМфxЕФКЏЪ§ЃЌЦфжаyЃЈЕЅЮЛЃКЁцЃЉБэЪОЫЎЯфжаЫЎЕФЮТЖШЃЎxЃЈЕЅЮЛЃКminЃЉБэЪОНгЭЈЕчдДКѓЕФЪБМфЃЎ
ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЯТБэМЧТМСЫ32minФк14ИіЪБМфЕуЕФЮТПиЫЎЯфжаЫЎЕФЮТЖШyЫцЪБМфxЕФБфЛЏЧщПі
НгЭЈЕчдДКѓЕФЪБМфxЃЈЕЅЮЛЃКminЃЉ | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | Ё |
ЫЎЯфжаЫЎЕФЮТЖШyЃЈЕЅЮЛЃКЁцЃЉ | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | Ё |
mЕФжЕЮЊ ЃЛ
ЃЈ2ЃЉЂйЕБ0ЁмxЁм4ЪБЃЌаДГівЛИіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪН ЃЛ
ЕБ4ЃМxЁм16ЪБЃЌаДГівЛИіЗћКЯБэжаЪ§ОнЕФКЏЪ§НтЮіЪН ЃЛ
ЂкШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫЩЯБэжаВПЗжЪ§ОнЖдгІЕФЕуЃЌИљОнУшГіЕФЕуЃЌЛГіЕБ0ЁмxЁм32ЪБЃЌЮТЖШyЫцЪБМфxБфЛЏЕФКЏЪ§ЭМЯѓЃК
ЃЈ3ЃЉШчЙћЫЎЮТyЫцЪБМфxЕФБфЛЏЙцТЩВЛБфЃЌдЄВтЫЎЮТЕк8ДЮДяЕН40ЁцЪБЃЌОрРыНгЭЈЕчдД minЃЎ