Question

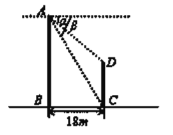
【题目】如图，半圆D的直径AB＝4，线段OA＝7，O为原点，点B在数轴的正半轴上运动，点B在数轴上所表示的数为m．

（1）当半圆D与数轴相切时，m＝　 ．

（2）半圆D与数轴有两个公共点，设另一个公共点是C．

①直接写出m的取值范围是　 ．

②当BC＝2时，求△AOB与半圆D的公共部分的面积．

（3）当△AOB的内心、外心与某一个顶点在同一条直线上时，求tan∠AOB的值．

Answer 1

【答案】（1）；（2）①；②△AOB与半圆D的公共部分的面积为；（3）tan∠AOB的值为或．

【解析】

（1）根据题意由勾股定理即可解答

（2）①根据题意可知半圆D与数轴相切时，只有一个公共点，和当O、A、B三点在数轴上时，求出两种情况m的值即可

②如图，连接DC，得出△BCD为等边三角形，可求出扇形ADC的面积，即可解答

（3）根据题意如图1，当OB＝AB时，内心、外心与顶点B在同一条直线上，作AH⊥OB于点H，设BH＝x，列出方程求解即可解答

如图2，当OB＝OA时，内心、外心与顶点O在同一条直线上，作AH⊥OB于点H，设BH＝x，列出方程求解即可解答

（1）当半圆与数轴相切时，AB⊥OB，

由勾股定理得m＝ ，

故答案为： ．

（2）①∵半圆D与数轴相切时，只有一个公共点，此时m＝，

当O、A、B三点在数轴上时，m＝7+4＝11，

∴半圆D与数轴有两个公共点时，m的取值范围为．

故答案为：．

②如图，连接DC，当BC＝2时，

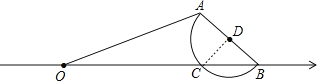
∵BC＝CD＝BD＝2，

∴△BCD为等边三角形，

∴∠BDC＝60°，

∴∠ADC＝120°，

∴扇形ADC的面积为 ，

，

∴△AOB与半圆D的公共部分的面积为 ；

（3）如图1，

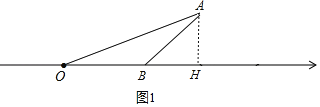
当OB＝AB时，内心、外心与顶点B在同一条直线上，作AH⊥OB于点H，设BH＝x，则72﹣（4+x）2＝42﹣x2，

解得x＝ ，OH＝ ，AH＝ ，

∴tan∠AOB＝，

如图2，当OB＝OA时，内心、外心与顶点O在同一条直线上，作AH⊥OB于点H，

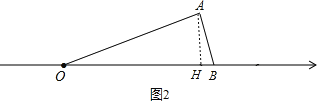
设BH＝x，则72﹣（4﹣x）2＝42﹣x2，

解得x＝ ，OH＝，AH＝，

∴tan∠AOB＝．

综合以上，可得tan∠AOB的值为或．