Question

【题目】直线与反比例函数（＞0）的图象分别交于点 A（，4）和点B（8，），与坐标轴分别交于点C和点D．

（1）求直线AB的解析式；

（2）观察图象，当时，直接写出的解集；

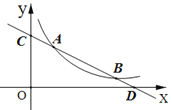
（3）若点P是轴上一动点，当△COD与△ADP相似时，求点P的坐标．

Answer 1

【答案】（1）；（2）2<x<8；（3）点P的坐标为（2，0）或（0，0）时，△COD与△ADP相似.

【解析】

（1）首先确定A、B两点坐标，再利用待定系数法即可解决问题；

（2）观察图象，根据A、B两点的横坐标即可确定．

（3）分两种情形讨论求解即可．

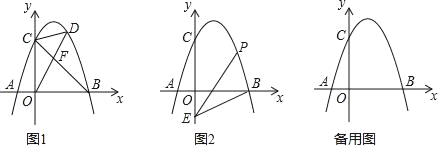
解：（1）∵点A（m,4）和点B（8,n)在图象上，

∴，即A（2，4），B（8，1）

把A（2，4），B（8，1）两点代入得

解得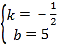：，所以直线AB的解析式为：

（2）由图象可得，当x>0时，的解集为2<x<8.

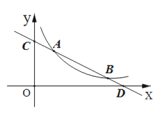
（3）由（1）得直线AB的解析式为，当x=0时，y=5，当y=0时，x=10，即C点坐标为（0，5），D点坐标为（10，0）

∴OC=5，OD=10，

∴

设P点坐标为（a，0），由题可以，点P在点D左侧，则PD=10-a

由∠CDO＝∠ADP可得

①当时，△COD∽△APD，此时AP∥CO，,解得a=2,

故点P坐标为（2，0）

②当时，△COD∽△PAD，即，解得a=0，

即点P的坐标为（0，0）

因此，点P的坐标为（2，0）或（0，0）时，△COD与△ADP相似.