��Ŀ����
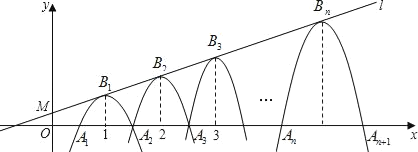
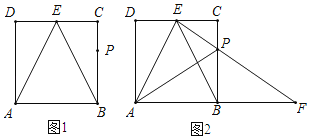
����Ŀ����ͼ1���ھ���ABCD�У�AB��2��AD��![]() ��E��CD���ϵ��е㣬P��BC���ϵ�һ�㣬��BP��2CP��
��E��CD���ϵ��е㣬P��BC���ϵ�һ�㣬��BP��2CP��
��1����֤����AED����BEC��
��2���ж�EB�Ƿ�ƽ�֡�AEC����˵�����ɣ�
��3����ͼ2������EP���ӳ���AB���ӳ����ڵ�F������AP�������Ӹ����ߣ���PFB�����ɶ�����P������α任����PAE���һ�����������Σ�ֱ��д�����ַ�����ָ���Գ��ᡢ��ת���ġ���ת�����ƽ�ƾ��룩��
���𰸡�(1)������;(2)������;(3)������.
��������
��1���ɾ��ε����ʵó�AD��BC��![]() ��CD��AB��2����D����C��90�������е�Ķ���ó�DE��CE��
��CD��AB��2����D����C��90�������е�Ķ���ó�DE��CE��![]() CD��1������SAS֤����ADE�ա�BCE�����ɵó����ۣ�
CD��1������SAS֤����ADE�ա�BCE�����ɵó����ۣ�
��2����������Ǻ��������AED��60�����ó���BEC����AED��60�������ɵó����ۣ�
��3�����жϳ���AEP�ա�FBP�����ɵó����ۣ�
��1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��![]() ��CD��AB��2����D����C��90����
��CD��AB��2����D����C��90����
��E��CD���ϵ��е㣬��DE��CE��![]() CD��1��
CD��1��
����ADE����BCE��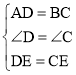 ��
��
���ADE�ա�BCE��SAS����
���AED����BEC��
��2���⣺EBƽ�֡�AEC���������£�
��Rt��ADE��AD��![]() ��DE��1��
��DE��1��
��tan��AED��![]() ��
��
���AED��60����
���BEC����AED��60����
���AEB��180������AED����BEC��60������BEC��
��EBƽ�֡�AEC��
��3���⣺��BP��2CP��BC��![]() ��
��
��CP��![]() ��BP��
��BP��![]() ��
��
��Rt��CEP��tan��CEP��![]() ��
��
���CEP��30����
���BEP��30����
���AEP��90����
��CD��AB��
���F����CEP��30����
��Rt��ABP��tan��BAP��![]() ��
��
���PAB��30����
���EAP��30������F����PAB��
��CB��AF��
��AP��FP����FBP��90������AEP��
����AEP����FBP��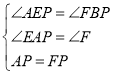 ��
��
���AEP�ա�FBP��AAS����
���PFB���ɶ�����P������α任����PAE���һ�����������Σ�
�任�ķ���Ϊ���ٽ���BPF�Ƶ�P˳ʱ����ת120������EPA�غϣ�����PE�۵���
�ڽ���BPF�Թ���P��ֱ��BC��ֱ���۵������Ƶ�P��ʱ����ת60����

 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�