题目内容
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
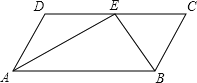
【答案】(1)当AD=BC时,四边形ABCD是平行四边形,理由见解析;(2)作出相应的图形见解析;(3)圆O的半径为2.5.
【解析】(1)添加条件AD=BC,利用一组对边平行且相等的四边形为平行四边形验证即可;
(2)作出相应的图形,如图所示;
(3)由平行四边形的对边平行得到AD与BC平行,可得同旁内角互补,再由AE与BE为角平分线,可得出AE与BE垂直,利用直径所对的圆周角为直角,得到AF与FB垂直,可得出两锐角互余,根据角平分线性质及等量代换得到∠AGF=∠AEB,根据sin∠AGF的值,确定出sin∠AEB的值,求出AB的长,即可确定出圆的半径.
(1)当AD=BC时,四边形ABCD是平行四边形,理由为:
证明:∵AD∥BC,AD=BC,
∴四边形ABCD为平行四边形;
故答案为:AD=BC;
(2)作出相应的图形,如图所示;
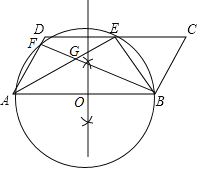
(3)∵AD∥BC,
∴∠DAB+∠CBA=180°,
∵AE与BE分别为∠DAB与∠CBA的平分线,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∵AB为圆O的直径,点F在圆O上,
∴∠AFB=90°,
∴∠FAG+∠FGA=90°,
∵AE平分∠DAB,
∴∠FAG=∠EAB,
∴∠AGF=∠ABE,
∴sin∠ABE=sin∠AGF=![]() ,
,
∵AE=4,
∴AB=5,
则圆O的半径为2.5.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.玩游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图;
(3)若该中学约有2400名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.