题目内容
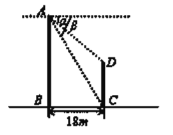
【题目】如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角![]() 为 30,测得C点的俯角
为 30,测得C点的俯角![]() 为 60° ,求建筑物CD的高度(结果保留根号).
为 60° ,求建筑物CD的高度(结果保留根号).
【答案】建筑物CD的高度为 ![]() m.
m.
【解析】
过点D作DE⊥AB于点E,依题可得:∠ACB=β=60°,∠ADE=α=30°,BC=18m,根据矩形性质得DE=BC=18m,CD=BE,在Rt△ABC中,根据正切函数的定义求得AB长 ;在Rt△ADE中,根据正切函数的定义求得AE长 ;由CD=BE=ABAE即可求得答案.
解:过点D作DE⊥AB于点E,则四边形BCDE是矩形,
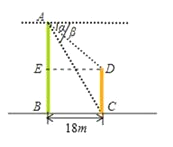
由题意得,∠ACB=β=60,∠ADE=α=30,BC=18m,
∴DE=BC=18m,CD=BE,
在Rt△ABC中,AB=BCtan∠ACB=18×tan60=![]() (m)
(m)
在Rt△ADE中,AE=DEtan∠ADE=18×tan30= ![]() (m)
(m)
∴CD=BE=ABAE= ![]() -
-![]() =
= ![]() (m)
(m)
答:建筑物CD的高度为 ![]() m.
m.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目