题目内容
【题目】在平面直角坐标系中,已知A(0,a)、B(b, 0),且a、b满足: ![]() ,点D为x正半轴上一动点
,点D为x正半轴上一动点
(1)求A、B两点的坐标
(2)如图,∠ADO的平分线交y轴于点C,点 F为线段OD上一动点,过点F作CD的平行线交y轴于点H,且∠AFH=45°, 判断线段AH、FD、AD三者的数量关系,并予以证明

(3)以AO为腰,A为顶角顶点作等腰△ADO,若∠DBA=30°,直接写出∠DAO的度数

【答案】(1)A(0,2),B(-2,0);(2)AH+FD=AD,证明详见解析; (3)∠DAO=60°,30°或150°.
【解析】试题分析: ![]() 根据所给式子求出
根据所给式子求出![]() 的值,即可表示出
的值,即可表示出![]() 的坐标.
的坐标.
![]() 在AD上取K使AH=AK,证明△AHF≌△AKF,得到
在AD上取K使AH=AK,证明△AHF≌△AKF,得到![]() 即可说明它们之间的关系.
即可说明它们之间的关系.
![]() 如图,可直接写出∠DAO的度数.
如图,可直接写出∠DAO的度数.
试题解析:
(1) ![]()
![]()
![]()
![]()
(2)AH+FD=AD,
在AD上取K使AH=AK,
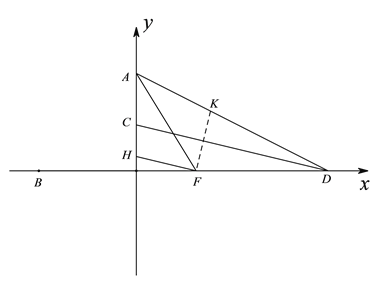
设∠HFO=α, ![]()
∵HF∥CD,∴∠CDO=∠ADC=α,
![]()
∴△AHF≌△AKF,
![]()
![]()
![]()
![]()
(3) ![]() 30°或150°.
30°或150°.
提示:如图所示:根据等腰三角形的性质进行计算即可.

练习册系列答案
相关题目