题目内容
【题目】已知正方形ABCD的边长为3,E是BC上一点,BE= ![]() ,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( )
,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA,点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为( ) 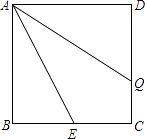
A.3 ![]() ﹣3
﹣3
B.3﹣ ![]()
C.![]()
D.3
【答案】A
【解析】解:如图所示: 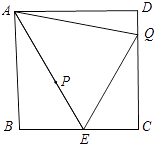
在Rt△ABE中,AE= ![]() =
= ![]() =2
=2 ![]() .
.
∵BC=3,BE= ![]() ,
,
∴EC=3﹣ ![]() .
.
由翻折的性质可知:PE=CE=3﹣ ![]() .
.
∵AP+PE≥AE,
∴AP≥AE﹣PE.
∴当点A、P、E一条直线上时,AP有最小值.
∴AP=AE﹣PE=2 ![]() ﹣(3﹣
﹣(3﹣ ![]() )=3
)=3 ![]() ﹣3.
﹣3.
故选:A.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目