题目内容
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I,IE⊥BC与E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】A
【解析】
①由I为△ABC三条角平分线的交点,IE⊥BC于E,得到∠ABI=∠IBD,由于∠CID+∠ABI=90°,即∠CIE+∠DIE+∠IBD=90°,于是得到∠BIE=∠CID;即①成立;②由I是△ABC三内角平分线的交点,得到点I到△ABC三边的距离相等,根据三角形的面积即可得到即②成立;③如图过I作IH⊥AB于H,IG⊥AC于G,有I是△ABC三内角平分线的交点,得到IE=IH=IG,通过Rt△AHT≌△RtAGI,得到AH=AG,同理BE=BF,CE=CG,于是得到即③成立;④由③证得IH=IE,∠FHI=∠IED=90°,于是得到△IHF与△DEI不一定全等,即④错误.
①∵I为△ABC角平分线的交点,IE⊥BC于E,
∴∠ABI=∠IBD,
∵∠DIC=∠DAC+∠ACI=![]() (∠BAC+∠ACB),∠ABI=
(∠BAC+∠ACB),∠ABI=![]() ∠ABC,
∠ABC,
∴∠CID+∠ABI=90°,
∵IE⊥BC于E,
∴∠BIE+∠IBE=90°,
∵∠ABI=∠IBE,
∴∠BIE=∠CID;
即①成立;
②∵I是△ABC三内角平分线的交点,
∴点I到△ABC三边的距离相等,
∴S△ABC=S△ABI+S△BCI+S△ACI=![]() ABIE+
ABIE+![]() BCIE+
BCIE+![]() ACIE=
ACIE=![]() IE(AB+BC+AC),即②成立;
IE(AB+BC+AC),即②成立;
③如图过I作IH⊥AB于H,IG⊥AC于G,
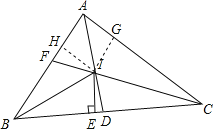
∵I是△ABC三内角平分线的交点,
∴IE=IH=IG,
在Rt△AHT与△RtAGI中,
![]() ,
,
∴Rt△AHT≌△RtAGI,
∴AH=AG,
同理BE=BH,CE=CG,
∴BE+BH=AB+BC-AH-CE=AB+BC-AC,
∴BE=![]() (AB+BC-AC);即③成立;
(AB+BC-AC);即③成立;
④由③证得IH=IE,
∵∠FHI=∠IED=90°,
∴△IHF与△DEI不一定全等,
∴HF不一定等于DE,
∴AC=AG+CG=AH+CE≠AF+CD,即④错误.
故选A.