Question

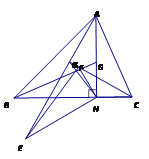
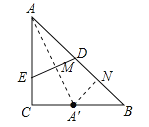
【题目】如图，△ABC中，∠C=90°，AC=BC=4，将△ABC翻折，使得点A落在BC的中点A'处，折痕分别交边AB、AC于点D、点E，那么AD：AE的值为_____．

Answer 1

【答案】

【解析】分析：连接AA′交DE于点M，过点A′作A′N⊥AB于点N，根据折叠的性质、勾股定理及相似三角形的性质可分别求出AD、AE的长度，将二者相比后即可得出结论．

详解：连接AA′交DE于点M，过点A′作A′N⊥AB于点N，如图所示．

∵AC=BC=4，∠C=90°，A′为线段BC的中点，

∴A′C=A′B=2，AA′==2，AB=4，

∴AM=AA′=，A′N=BN=，

∴AN=AB﹣BN=3．

∵∠EAM=∠A′AC，∠AME=∠C，

∴△AEM∽△AA′C，∴=，∴AE=．

同理：△ADM∽△AA′N，∴=，

∴AD==．

故答案为：．