题目内容
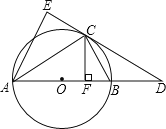
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )

A. 2![]() B. 2
B. 2![]() C.
C. ![]() +1D.
+1D. ![]() ﹣1
﹣1
【答案】A
【解析】
连接BD交AP于O,作PE⊥BC于E,连接OE,由等腰三角形的性质得出∠PBE=30°,BE=CE,由直角三角形的性质得出PE=![]() PB=1,由平行四边形的性质得出OP=OA=1,OB=OD,得出OE是△BCD的中位线,得出CD=2OE,由勾股定理得:OE=
PB=1,由平行四边形的性质得出OP=OA=1,OB=OD,得出OE是△BCD的中位线,得出CD=2OE,由勾股定理得:OE=![]() =
=![]() ,即可得出结果.
,即可得出结果.
连接BD交AP于O,作PE⊥BC于E,连接OE,如图所示:
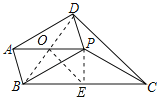
∵PB=PC=2,∠BPC=120°,PE⊥BC,
∴∠PBE=30°,BE=CE,
∴PE=![]() PB=1,
PB=1,
∵四边形ABPD是平行四边形,
∴OP=OA=1,OB=OD,
∴OE是△BCD的中位线,
∴CD=2OE,
∵PA∥BC,
∴PA⊥PE,
∴∠APE=90°,
由勾股定理得:OE=![]() =
=![]() ,
,
∴CD=2OE=2![]() ;
;
故选A.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目