题目内容
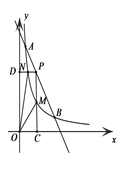
【题目】如图，一次函数与反比例函数的图像交于A（1，12）和B（6，2）两点。点P是线段AB上一动点（不与点A和B重合），过P点分别作x、y轴的垂线PC、PD交反比例函数图像于点M、N，则四边形PMON面积的最大值是（ ）
A. 
B. 
C. 6 D. 12
【答案】A
【解析】解：设反比例函数解析式为y=
，一次函数解析式为y=ax+b，将点A（1，12）代入y=
中，得k=12，∴反比例函数解析式为y=
，将点A（1，12）、B（6，2）代入y=ax+b中，得
，解得
，∴一次函数解析式为y=﹣2x+14．
设点P的坐标为（m，14﹣2m），则S四边形PMON=S矩形OCPD﹣S△OCM﹣S△ODN=S矩形OCPD﹣|k|=m（14﹣2m）﹣12=﹣2m2+14m﹣12=﹣2
+
，∴四边形PMON面积的最大值是
．
故选A．
练习册系列答案
相关题目
