题目内容
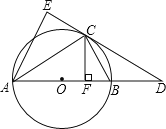
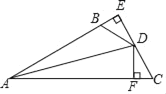
【题目】如图,AD平分∠EAC,DE⊥AB于E,DF⊥AC于F,BD=CD,
(1)求证:BE=FC;
(2)已知AC=20,BE=4,求AB的长.
【答案】(1)详见解析;(2)12
【解析】
(1)根据角平分线性质和全等三角形的性质即可解决问题;
(2)由△ADE≌△ADF(AAS),推出AF=AE,由BE=CF=4,AC=20,推出AF=AE=20﹣4=16即可解决问题;
(1)∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△BED和Rt△CFD中
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)在△ADE和△ADF中,
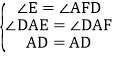 ,
,
∴△ADE≌△ADF(AAS),
∴AF=AE,
∵BE=CF=4,AC=20,
∴AF=AE=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.

练习册系列答案
相关题目