��Ŀ����
����Ŀ��ij��ѧ��չ����ѧʷ��֪ʶ����������꼶��1������2������ݳ����ɼ�����ѡ��5��ѡ�ֲμӸ������������ѡ����5��ѡ�ֵĸ����ɼ�������Ϊ100�֣���ͼ��ʾ��
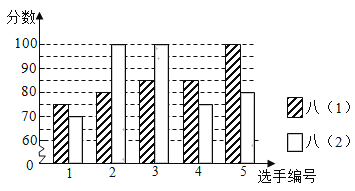
��1������ͼʾ��д�±�a��b��c��ֵ��
ͳ���� ��� | ƽ�������֣� | ��λ�����֣� | �������֣� |
���꣨1���� | a | 85 | c |
���꣨2���� | 85 | b | 100 |
��2��������ิ���ɼ���ƽ��������λ���������ĸ����ѡ�ڸ����ɼ��Ϻã�
��3��ͨ��������꣨1����5��ѡ�ֵĸ����ɼ��ķ���S�ˣ�1��2��70�����������꣨2����5��ѡ�ָ����ɼ��ķ���ж��ĸ����ѡ�ָ����ɼ���Ϊ���⣮
���𰸡���1��a��85�֣�b��80�֣�c��85�֣���2�����꣨1����ɼ���Щ����3�����꣨2����
��������
��1���ֱ������꣨1�����ƽ���ֺ�����������ɣ�
��2�������������ƽ������ȣ����Դ���λ���ĽǶ�ȥ�����������༶�ijɼ���
��3���ֱ��������ݴ�����Ŀ�ṩ�ķ��ʽ���м��㼴�ɣ�
�⣺��1��a����75+80+85+85+100����5��85�֣�
c��85�֣�
���մ�С�����˳������Ϊ��70��75��80��100��100��b��80�֣�
������£�
ͳ���� ��� | ƽ�������֣� | ��λ�����֣� | �������֣� |
���꣨1���� | 85 | 85 | 85 |
���꣨2���� | 85 | 80 | 100 |
��2�����꣨1����ɼ���Щ����Ϊ�����༶��ƽ������ͬ�����꣨1�������λ���ߣ�
������ƽ������ͬ���������λ���ߵİ��꣨1����ɼ���Щ��
��3��S�ˣ�2��2��![]() [��70��85��2+2����100��85��2+��75��85��2+��80��85��2]��160��
[��70��85��2+2����100��85��2+��75��85��2+��80��85��2]��160��
��S�ˣ�1��2��70��
��S�ˣ�1��2��S�ˣ�2��2��
����꣨2�����ѡ�ָ����ɼ���Ϊ���⣮

 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�����Ŀ��ij�̳���Ϊ�������˿ͣ�������ɫ���˽�������ٰ�����Ʒ�н���������������200Ԫ�ߣ������ֽ���������ѡ��һ��ֱ�ӻ��20Ԫ�����ȯ�����ǵõ�һ��ҡ���Ļ��ᣮ��֪��ҡ������װ��2�������2��������ɫ����������ͬ��ҡ���߱����ҡ������һ������ҡ���������������ɫ����������������ȯ�Ķ��٣�
�� | ���� | һ��һ�� | ���� |
���ȯ��Ԫ�� | 18 | 24 | 18 |
��1���������б���������״ͼ������һ������ҡ��һ��һ������ĸ��ʣ�
��2�����һ���˿͵����ڱ��깺����200Ԫ����ֻ���ǻ��������Ʒȯ�������������ѡ�����ַ�����Ϊʵ�ݣ�