题目内容
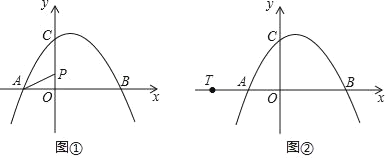
【题目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=![]() 正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
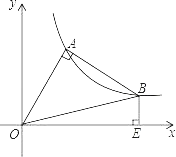
A. 3B. 2C. 3D. 4
【答案】D
【解析】
过点A作AF⊥y轴于点F,延长EB交FA的延长线于点D.由题意可证四边形DEOF是矩形,可得DE=OF,DF=OE,由题意可证△AFO≌△BDA,可得AF=DB, AD=OF,设出A点坐标,表示出BE与OE,即可求出所求式子的值.
如图:过点A作AF⊥y轴于点F,延长EB交FA的延长线于点D.
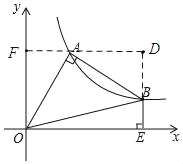
∵AF⊥OF,BE⊥OE,OE⊥OF
∴四边形DEOF是矩形
∴∠D=90°,OF=DE,DF=OE
设点A(a,![]() ),即AF=a,OF=
),即AF=a,OF=![]()
∵∠BAO=90°,AF⊥FO
∴∠BAD+∠FAO=90°,∠FAO+∠FOA=90°
∴∠DAB=∠AOF且AO=AB,∠AFO=∠ADB=90°
∴△AFO≌△BDA(AAS)
∴AD=OF=![]() ,DB=AF=a
,DB=AF=a
∴BE=DE﹣DB=![]() ﹣a,OE=DF=AF+AD=a+
﹣a,OE=DF=AF+AD=a+![]()
∴OE2﹣BE2=(a+![]() )2﹣(
)2﹣(![]() ﹣a)2=4
﹣a)2=4
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目