��Ŀ����
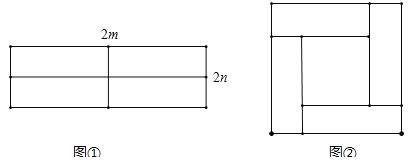
����Ŀ����ͼ��ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ��ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ���������Σ�
��1��ͼ���еĴ������εı߳������� ����ͼ���е�С�����εı߳������� ����
��2��ͼ���еĴ������ε���������� ����ͼ���е�С�����ε���������� ����ͼ����ÿ��С�����ε�������� ����
��3���۲�ͼ�ڣ�����д����m+n��2����m��n��2��mn����������ʽ��ĵ�����ϵ���� ����
���𰸡���1��m+n��m��n����2����m+n��2����m��n��2��mn����3����m+n��2����m��n��2��4mn��
��������
��1������С�����εı߳������ɵõ��������εı߳��Լ�С�����εı߳���
��2�����������εı߳����ɵõ������ε����������С�����εı߳������ɵõ�С�����ε������
��3�����ݴ������ε������ȥС�����ε���������ĸ�С�����ε����֮�ͣ����ɵõ���������ʽ��ĵ�����ϵ��
�⣺��1��ͼ���еĴ������εı߳�����m+n��ͼ���е�С�����εı߳�����m��n��
�ʴ�Ϊ��m+n��m��n��
��2��ͼ���еĴ������ε�������ڣ�m+n��2��ͼ���е�С�����ε�������ڣ�m��n��2��ͼ����ÿ��С�����ε������mn��
�ʴ�Ϊ����m+n��2����m��n��2��mn��
��3����ͼ���ɵã���m+n��2����m��n��2��mn����������ʽ��ĵ�����ϵΪ����m+n��2����m��n��2��4mn��
�ʴ�Ϊ����m+n��2����m��n��2��4mn��