题目内容
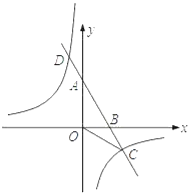
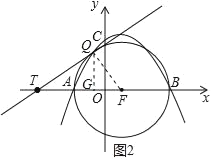
【题目】如图①,抛物线y=ax2+bx+c经过点A(﹣2,0)、B(4,0)、C(0,3)三点.
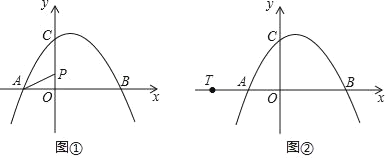
(1)试求抛物线的解析式;
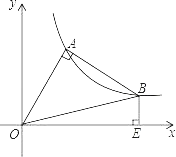
(2)点P是y轴上的一个动点,连接PA,试求5PA+4PC的最小值;
(3)如图②,若直线l经过点T(﹣4,0),Q为直线l上的动点,当以A、B、Q为顶点所作的直角三角形有且仅有三个时,试求直线l的解析式.
【答案】(1)![]() ;(2)5PA+4PC的最小值为18;(3)直线l的解析式为
;(2)5PA+4PC的最小值为18;(3)直线l的解析式为![]() 或
或![]() .
.
【解析】
(1)设出交点式,代入C点计算即可 (2)连接AC、BC,过点A作AE⊥BC于点E,过点P作PD⊥BC于点D,易证△CDP∽△COB,得到比例式![]() ,得到PD=
,得到PD=![]() PC,所以5PA+4PC=5(PA+
PC,所以5PA+4PC=5(PA+![]() PC)=5(PA+PD),当点A、P、D在同一直线上时,5PA+4PC=5(PA+PD)=5AE最小,利用等面积法求出AE=
PC)=5(PA+PD),当点A、P、D在同一直线上时,5PA+4PC=5(PA+PD)=5AE最小,利用等面积法求出AE=![]() ,即最小值为18 (3)取AB中点F,以F为圆心、FA的长为半径画圆, 当∠BAQ=90°或∠ABQ=90°时,即AQ或BQ垂直x轴,所以只要直线l不垂直x轴则一定找到两个满足的点Q使∠BAQ=90°或∠ABQ=90°,即∠AQB=90°时,只有一个满足条件的点Q,∴直线l与⊙F相切于点Q时,满足∠AQB=90°的点Q只有一个;此时,连接FQ,过点Q作QG⊥x轴于点G,利用cos∠QFT求出QG,分出情况Q在x轴上方和x轴下方时,分别代入直接l得到解析式即可
,即最小值为18 (3)取AB中点F,以F为圆心、FA的长为半径画圆, 当∠BAQ=90°或∠ABQ=90°时,即AQ或BQ垂直x轴,所以只要直线l不垂直x轴则一定找到两个满足的点Q使∠BAQ=90°或∠ABQ=90°,即∠AQB=90°时,只有一个满足条件的点Q,∴直线l与⊙F相切于点Q时,满足∠AQB=90°的点Q只有一个;此时,连接FQ,过点Q作QG⊥x轴于点G,利用cos∠QFT求出QG,分出情况Q在x轴上方和x轴下方时,分别代入直接l得到解析式即可
解:(1)∵抛物线与x轴交点为A(﹣2,0)、B(4,0)
∴y=a(x+2)(x﹣4)
把点C(0,3)代入得:﹣8a=3
∴a=﹣![]()
∴抛物线解析式为y=﹣![]() (x+2)(x﹣4)=﹣
(x+2)(x﹣4)=﹣![]() x2+
x2+![]() x+3
x+3
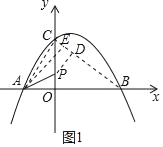
(2)连接AC、BC,过点A作AE⊥BC于点E,过点P作PD⊥BC于点D
∴∠CDP=∠COB=90°
∵∠DCP=∠OCB
∴△CDP∽△COB
∴![]()
∵B(4,0),C(0,3)
∴OB=4,OC=3,BC=![]() =5
=5
∴PD=![]() PC
PC
∴5PA+4PC=5(PA+![]() PC)=5(PA+PD)
PC)=5(PA+PD)
∴当点A、P、D在同一直线上时,5PA+4PC=5(PA+PD)=5AE最小
∵A(﹣2,0),OC⊥AB,AE⊥BC
∴S△ABC=![]() ABOC=
ABOC=![]() BCAE
BCAE
∴AE=![]()
∴5AE=18
∴5PA+4PC的最小值为18.
(3)取AB中点F,以F为圆心、FA的长为半径画圆
当∠BAQ=90°或∠ABQ=90°时,即AQ或BQ垂直x轴,
∴只要直线l不垂直x轴则一定找到两个满足的点Q使∠BAQ=90°或∠ABQ=90°
∴∠AQB=90°时,只有一个满足条件的点Q
∵当Q在⊙F上运动时(不与A、B重合),∠AQB=90°
∴直线l与⊙F相切于点Q时,满足∠AQB=90°的点Q只有一个
此时,连接FQ,过点Q作QG⊥x轴于点G
∴∠FQT=90°
∵F为A(﹣2,0)、B(4,0)的中点
∴F(1,0),FQ=FA=3
∵T(﹣4,0)
∴TF=5,cos∠QFT=![]()
∵Rt△FGQ中,cos∠QFT=![]()
∴FG=![]() FQ=
FQ=![]()
∴xQ=1﹣![]() ,QG=
,QG=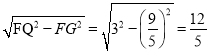
①若点Q在x轴上方,则Q(![]() )
)
设直线l解析式为:y=kx+b
∴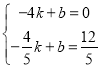 解得:
解得:![]()
∴直线l:![]()
②若点Q在x轴下方,则Q(![]() )
)
∴直线l:![]()
综上所述,直线l的解析式为![]() 或
或![]()

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
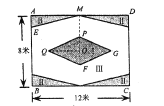
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,