题目内容
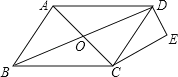
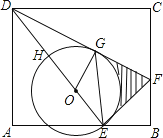
【题目】如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,![]() ≈1.73,π≈3.14).
≈1.73,π≈3.14).
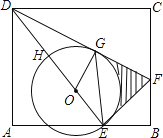
【答案】(1)见解析;(2)图中阴影部分的面积约为6.2.
【解析】
(1)由条件可证∠AED=∠EFB,从而可证△ADE∽△BEF.
(2)由DF与⊙O相切,DH=OH=OG=3可得∠ODG=30°,从而有∠GOE=120°,并可求出DG、EF长,从而可以求出△DGO、△DEF、扇形OEG的面积,进而可以求出图中阴影部分的面积.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠AED=90°﹣∠BEF=∠EFB.
∵∠A=∠B,∠AED=∠EFB,
∴△ADE∽△BEF.
(2)解:∵DF与⊙O相切于点G,
∴OG⊥DG.
∴∠DGO=90°.
∵DH=OH=OG,
∴sin∠ODG=![]() .
.
∴∠ODG=30°.
∴∠GOE=120°.
∴S扇形OEG=![]() =3π.
=3π.
在Rt△DGO中,
cos∠ODG=![]() .
.
∴DG=3![]() .
.
在Rt△DEF中,
tan∠EDF=![]() .
.
∴EF=3![]() .
.
∴S△DEF=![]() ,
,
S△DGO=![]() .
.
∴S阴影=S△DEF﹣S△DGO﹣S扇形OEG
=![]() ﹣3π
﹣3π
=.9![]() ﹣3π
﹣3π
≈9×1.73﹣3×3.14
=6.15
≈6.2
∴图中阴影部分的面积约为6.2.

【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.
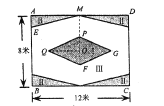
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,