题目内容
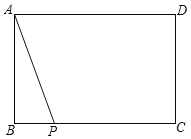
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)想办法证明∠B=∠DAF,∠BAE=∠ADF即可解决问题.
(2)只要证明四边形ADEB是平行四边形即可解决问题.
(1)∵AD∥BC,
∴∠DAC=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAF=∠B,
∵∠AEC=∠AED+∠DEC=∠B+∠BAE,∠AED=∠CAD=∠ACB,
∴∠DEC=∠BAE,
∵AD∥BC,
∴∠DEC=∠ADF,
∴∠BAE=∠ADF,
∴△ABE∽△DAF.
(2)∵ACFC=AEEC,AC=AB,
∴ABFC=AEEC,
∴![]() ,
,
∵∠B=∠FCE,∠BAE=∠FEC,
∴△BAE∽△CEF,
∴![]() ,
,
∴![]() ,
,
∴FC=EF,
∴∠FEC=∠FCE,
∵∠FCE=∠B,
∴∠B=∠FEC,
∴AB∥DE,
∵AD∥BE,
∴四边形ADEB是平行四边形,
∴AD=BE.

练习册系列答案
相关题目