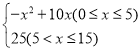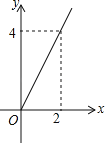题目内容
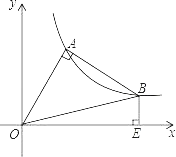
【题目】如图,在平面直角坐标系中,直线y=![]() x+6与x、y轴分别交于点A,点B,双曲线的解析式为
x+6与x、y轴分别交于点A,点B,双曲线的解析式为![]()

(1)求出线段AB的长
(2)在双曲线第四象限的分支上存在一点C,使得CB⊥AB,且CB=AB,求k的值;
(3)在(1)(2)的条件下,连接AC,点D为BC的中点,过D作AC的垂线BF,交AC于B,交直线AB于F,连AD,若点P为射线AD上的一动点,连接PC、PF,当点P在射线AD上运动时,PF![]() -PC
-PC![]() 的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
【答案】(1)10(2)-12;(3)不变,25
【解析】
(1)首先求出图象与坐标轴交点坐标,进而得出AO,OB的长,即可利用勾股定理求出AB的长;
(2)首先作CD⊥y轴于点D,求出∠BAO=∠CBD再利用△ABO≌△BDC,进而得出C点坐标,即可得出k的值
(3)首先连接FC交AP于M,利用△ABD≌△CBF(SAS),得出∠BAD=∠DCM,进而利用勾股定理求出PF![]() -PC
-PC![]() =DF
=DF![]() -CD
-CD![]() ,求出即可
,求出即可
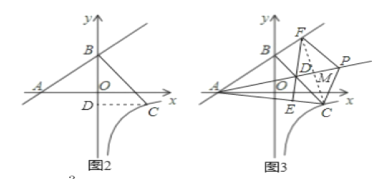
(1)
由y=![]() x+6与x、y轴分別交于点A,点B,
x+6与x、y轴分別交于点A,点B,
得:x=0时,y=6,y=0时,x=-8
故A(-8,0),B(0,6)
∴AO=8, OB=6
∴AB=![]() =10
=10
(2)作CD⊥y轴于点D,
∵∠ABO+∠BAO=90°,∠CBO+∠ABO=90°,
∴∠BAO=∠CBD
在△ABO和△BDC中,
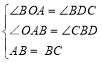
∴△ABO≌△BDC(AAS),
∴CD=OB=6, BD=OA=8
∴OD=BD-OB=8-6=2
∴C(6,-2)
∴k=6×(-2)=-12
(3)连接FC交AP于M
∵AB=BC,∠ABC=90°,
∴∠ACB=45°
∵EF⊥AC
∴∠BDR=∠EDC=45°
∵∠ABC=90°
∴.∠BFD=∠BDF=45°
∴BD=BF
在△ABD和△CBF中
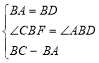
∴△ABD≌△CBF(SAS)
∴∠BAD=∠DCM
∴∠DMC=∠ABD=90°
∴PF![]() -PC
-PC![]() =(FM
=(FM![]() + MP
+ MP![]() )-(CM
)-(CM![]() +MP
+MP![]() )=FM
)=FM![]() -CM
-CM![]() =(DF
=(DF![]() -DM
-DM![]() )-(CD
)-(CD![]() -DM
-DM![]() )=DF
)=DF![]() -CD
-CD![]()
∵D是BC的中点
∴BD=CD=5
.∴BF=5
∴DF=![]() =5
=5![]()
∴PF![]() -PC
-PC![]() =(5
=(5![]() )
) ![]() -5
-5![]() =25
=25

 阅读快车系列答案
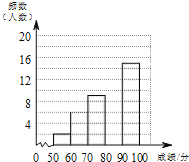
阅读快车系列答案【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?