题目内容
【题目】问题背景:某数学兴趣小组把两个等腰直角三角形的直角顶点重合,发现了一些有趣的结论.
结论一:
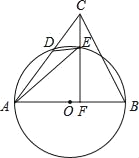
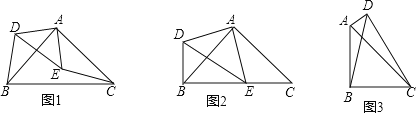
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE,试说明△ADB≌△AEC;
结论二:
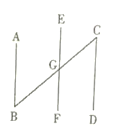
(2)如图2,在(1)的条件下,若点E在BC边上,试说明DB⊥BC;
应用:
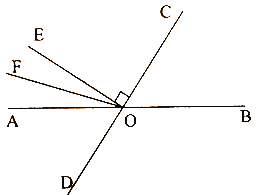
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,∠BAD+∠BCD=180°,连接BD,BD=7cm,求四边形ABCD的面积.
【答案】(1)见解析;(2)见解析;(3)S四边形ABCD=24.5(cm2).
【解析】
(1)根据全等三角形的判定SAS进行证明即可得到答案;
(2)根据全等三角形的性质和三角形内角和定理进行计算,即可得到答案;
(3)作BE⊥BD,交DC的延长线于点E,根据三角形内角和和全等三角形的判定定理(ASA),即可得到答案.
(1)∵∠BAC=∠DAE=90°,
∴∠BAE+∠CAE=∠BAE+∠BAD,
∴∠CAE=∠BAD,
又∵AB=AC,AD=AE,
∴△ADB≌△AEC(SAS);
(2)由(1)得△ADB≌△AEC,
∴∠C=∠ABD,
又∵∠ABC+∠C=90°,
∴∠ABC+∠ABD=90°,
∴DB⊥BC;
(3)作BE⊥BD,交DC的延长线于点E,
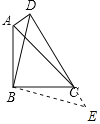
∵BE⊥BD,
∴∠CBE+∠DBC=90°,
又∵∠ABD+∠DBC=90°,
∴∠ABD=∠EBC,
∵∠BAD+∠BCD=180°,
∠BCE+∠BCD=180°,
∴∠BAD=∠BCE,
又∵BA=BC,
∴△BAD≌△BCE(ASA),
∴BD=BE,且S△BAD=S△BCE,
∴S四边形ABCD=S△ABD+S△DBC
=S△BCE+S△BCD
=S△BDE
=![]() ×7×7=24.5(cm2).
×7×7=24.5(cm2).