题目内容
【题目】如图,直角坐标系中,点 A( 2,2)、B(0,1)点 P 在 x 轴上,且△PAB 的等腰三角形,则满足条件的点 P 共有()个

A.1B.2C.3D.4
【答案】D
【解析】
由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
如图,点A(-2,2)、B(0,1),
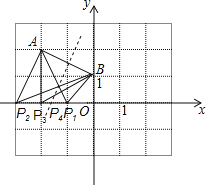
①以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=-![]() ,
,
∴P4(-![]() ,0).
,0).
∴符合条件的点有4个.
故选:D.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目