题目内容
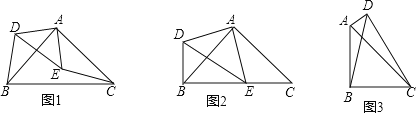
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

【答案】(1)150°;(2)2
【解析】分析:(1)先根据三角形内角和计算出∠BAC=150°,然后利用旋转的定义可判断旋转中心为点A,旋转角为150°;(2)根据旋转的性质得到∠DAE=∠BAC=150°,AB=AD=4,AC=AE,利用周角定义可得到∠BAE=60°,然后利用点C为AD中点得到AC=![]() AD=2,于是得到AE=2.
AD=2,于是得到AE=2.
本题解析:
解:(1)在△ABC中,∵∠B+∠ACB=30°, ∴∠BAC=150°,
当△ABC逆时针旋转一定角度后与△ADE重合,
∴旋转中心为点A,∠BAD等于旋转角,即旋转角为150°;
(2)∵△ABC绕点A逆时针旋转150°后与△ADE重合,
∴∠DAE=∠BAC=150°,AB=AD=4,AC=AE, ∴∠BAE=360°-150°-150°=60°,
∵点C为AD中点, ∴AC=![]() AD=2, ∴AE=2.
AD=2, ∴AE=2.

练习册系列答案
相关题目