��Ŀ����
����Ŀ���Ķ����⣺��֪������ʵ��a��0��b��0������a+b��2![]() �����ҽ���a = bʱ���Ⱥų�������ʱȡ�ô���ʽa+b����Сֵ��
�����ҽ���a = bʱ���Ⱥų�������ʱȡ�ô���ʽa+b����Сֵ��
�������Ͻ��ۣ�����������⣺
(1)��չ����a>0�����ҽ���a=___ʱ��a+![]() ����Сֵ����СֵΪ____��
����Сֵ����СֵΪ____��
(2)Ӧ�ã�
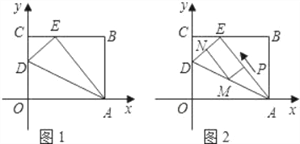
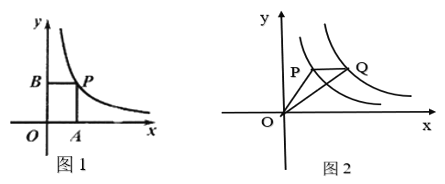
����ͼ1����֪��PΪ˫����y=![]() (x>0)�ϵ�����һ�㣬����P��PA��x�ᣬPB�Ay�ᣬ�ı���OAPB���ܳ�ȡ����Сֵʱ�������P�������Լ��ܳ���Сֵ��
(x>0)�ϵ�����һ�㣬����P��PA��x�ᣬPB�Ay�ᣬ�ı���OAPB���ܳ�ȡ����Сֵʱ�������P�������Լ��ܳ���Сֵ��
����ͼ2����֪��Q��˫����y=![]() (x>0)��һ�㣬��PQ��x�ᣬ ����OP��OQ�����߶�OPȡ����Сֵʱ����ƽ����ȡһ��C��ʹ����0��P��Q��CΪ������ı�����ƽ���ı��Σ������C�����꣮
(x>0)��һ�㣬��PQ��x�ᣬ ����OP��OQ�����߶�OPȡ����Сֵʱ����ƽ����ȡһ��C��ʹ����0��P��Q��CΪ������ı�����ƽ���ı��Σ������C�����꣮
���𰸡���1��1��2����2��P(2��2)���ܳ���С8����3����-2��0������2��0����6��4����
��������
��1������������Ķ���ֱ�Ӵ�����㼴�ɣ�
��2�����������㣬���ݵ�һ�ʵó��Ľ���ֱ��Ӧ�ã�
����������˼·����������P���ٸ�����ȫƽ����ʽ���μ��ɣ����P�����������Q�㣬���ɸ���ƽ���ı����������C�����꣮
��1����������֪a=![]() ʱ��С���֡�a>0����a=1����a+
ʱ��С���֡�a>0����a=1����a+![]() =2��
=2��
��2�������P(x��![]() )����x>0�������ı���OAPB�ܳ�Ϊ2��x+
)����x>0�������ı���OAPB�ܳ�Ϊ2��x+![]() ����
����
��x=![]() ʱ��x=2����ʱ2��x+
ʱ��x=2����ʱ2��x+![]() ������Сֵ8�����ܳ���СΪ8����ʱ��P(2��2)��
������Сֵ8�����ܳ���СΪ8����ʱ��P(2��2)��
�����P(x��![]() )����x>0����OP=
)����x>0����OP=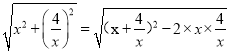 =
=![]() ��
��
OP������x+![]() ��������x=
��������x=![]() ����x=2������P��2��2����
����x=2������P��2��2����
�ɵ�P��2��2��������֪Q����������2������y=![]() (x>0)�õ�Q��4��2����
(x>0)�õ�Q��4��2����
������O��P��Q�������꣬ҪʹOPQC�ĵ��ܹ���ƽ���ı��Σ����C����Ϊ��
��-2��0������2��0����6��4����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�