Question

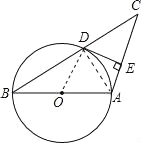
【题目】如图所示，已知AB是圆O的直径，圆O过BC的中点D，且DE⊥AC．

（1）求证：DE是圆O的切线；

（2）若∠C=30°，CD=10cm，求圆O的半径．

Answer 1

【答案】

【解析】

试题分析：（1）连接OD，利用三角形的中位线定理可得出OD∥AC，再利用平行线的性质就可证明DE是圆O的切线．

（2）利用30°特殊角度，可求出AD的长，由两直线平行同位角相等，可得出∠ODB=∠C=30°，从而△ABD为直角三角形，圆O的半径可求．

试题解析：（1）连接OD，∵D是BC的中点，O为AB的中点，∴OD∥AC．

又∵DE⊥AC，∴OD⊥DE，∵OD为半径，∴DE是圆O的切线．

（2）连接AD；∵AB是圆O的直径，∴∠ADB=90°=∠ADC，

∴△ADC是直角三角形．∵∠C=30°，CD=10，∴AD=．

∵OD∥AC，OD=OB，∴∠B=30°，∴△OAD是等边三角形，∴OD=AD=，

∴圆O的半径为cm．