Question

【题目】对于平面直角坐标系xOy中的点M和图形W1，W2给出如下定义：点P为图形W1上一点，点Q为图形W2上一点，当点M是线段PQ的中点时，称点M是图形W1，W2的“中立点”．如果点P（x1，y1），Q（x2，y2），那么“中立点”M的坐标为（，）．

已知，点A（-3，0），B（0，4），C（4，0）．

（1）连接BC，在点D（，0），E（0，1），F（0，）中，可以成为点A和线段BC的“中立点”的是______；

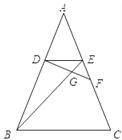
（2）已知点G（3，0），⊙G的半径为2，如果直线y=-x+1存在点K可以成为点A和⊙G的“中立点”，求点K的坐标；

（3）以点C为圆心，半径为2作圆，点N为直线y=2x+4上的一点，如果存在点N，使得y轴上的一点可以成为点N与⊙C的“中立点”，直接写出点N的横坐标的取值范围．

Answer 1

【答案】（1）D、F；（2）点K坐标为（1，0）或（0，1）；（3）-6≤xN≤-2

【解析】

（1）根据新定义，点A和线段BC的“中立点”是点D、F；

（2）点A和⊙G的“中立点”在以点O为圆心、半径为1的圆上运动，因为点K在直线y=-x+1上，设出点K坐标，求解即可；

（3）根据题意可得，点N与圆C的“中立点”在以线段NC的中点P为圆心、半径为1的圆上运动，⊙P与y轴相切时，即可求得其取值范围.

（1）如图1中，

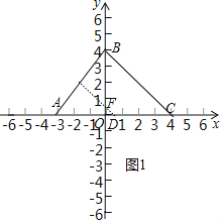
观察图象可知，满足条件的点在△ABC的平行于BCD的中位线上，

故成为点A和线段BC的“中立点”的是D、F．

故答案为D、F；

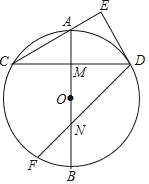
（2）如图2中，点A和⊙G的“中立点”在以O为圆心，1为半径的圆上运动，

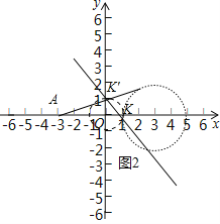
因为点K在直线y=-x+1上，设K（m，-m+1），

则有m2+（-m+1）2=1，

解得m=0或1，

∴点K坐标为（1，0）或（0，1）．

（3）如图3中，由题意，当点N确定时，点N与⊙G的“中立点”是以NC的中点P为圆心1为半径的⊙P，

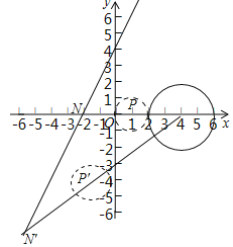
当⊙P与y轴相切时，点N的横坐标分别为-2或-6，

所以满足条件的点N的横坐标的取值范围为-6≤xN≤-2．