题目内容
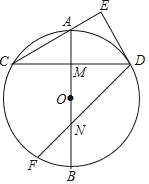
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
【答案】(1)60;(2)证明见解析;(3)![]() .
.
【解析】
(1)由CD⊥AB和M是OA的中点,利用三角函数可以得到∠DOM=60°,进而得到△OAD是等边三角形,∠OAD=60°.
(2)只需证明DE⊥OD.便可以得到DE与⊙O相切.
(3)利用圆的综合知识,可以证明,∠CND=90°,∠CFN=60°,根据特殊角的三角函数值可以得到FN的数值.
解:(1)如图1,连接OD,AD

∵AB是⊙O的直径,CD⊥AB
∴AB垂直平分CD
∵M是OA的中点,
∴OM=![]() OA=
OA=![]() OD
OD
∴cos∠DOM=![]() =
=![]() ,
,
∴∠DOM=60°
又:OA=OD
∴△OAD是等边三角形
∴∠OAD=60°
故答案为:60°
(2)∵CD⊥AB,AB是⊙O的直径,
∴CM=MD.
∵M是OA的中点,
∴AM=MO.
又∵∠AMC=∠DMO,
∴△AMC≌△OMD.
∴∠ACM=∠ODM.
∴CA∥OD.
∵DE⊥CA,
∴∠E=90°.
∴∠ODE=180°﹣∠E=90°.
∴DE⊥OD.
∴DE与⊙O相切.
(3)如图2,连接CF,CN,

∵OA⊥CD于M,
∴M是CD中点.
∴NC=ND.
∵∠CDF=45°,
∴∠NCD=∠NDC=45°.
∴∠CND=90°.
∴∠CNF=90°.
由(1)可知∠AOD=60°.
∴∠ACD=![]() ∠AOD=30°.
∠AOD=30°.
在Rt△CDE中,∠E=90°,∠ECD=30°,DE=3,
∴CD=![]() ,
,
在Rt△CND中,∠CND=90°,∠CDN=45°,CD=6,
∴CN=CD·sin45°=3![]() .
.
由(1)知∠CAD=2∠OAD=120°,
∴∠CFD=180°﹣∠CAD=60°.
在Rt△CNF中,∠CNF=90°,∠CFN=60°,CN=3![]() ,
,
∴FN=![]() .
.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案