��Ŀ����
����Ŀ��ijʳƷ������һ�ְ��Ʒʳ�ģ��ɱ�Ϊ2Ԫ/ǧ�ˣ�ÿ��IJ���P����ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ����㺯����ϵʽp��![]() x+8�����г���������Ϣ���֣���ʳ��ÿ����г�������q����ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
x+8�����г���������Ϣ���֣���ʳ��ÿ����г�������q����ǧ�ˣ������ۼ۸�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���������������
���ۼ۸�x��Ԫ/ǧ�ˣ� | 2 | 4 | ���� | 10 |
�г�������q����ǧ�ˣ� | 12 | 10 | ���� | 4 |
��֪����۲��Ź涨���ۼ۸�x������2Ԫ/ǧ���Ҳ�����10Ԫ/ǧ�ˣ�
��1��ֱ��д��q��x�ĺ�����ϵʽ����ע���Ա���x��ȡֵ��Χ��
��2����ÿ��IJ���С�ڻ�����г�������ʱ������ʳ����ȫ���۳�����ÿ��IJ��������г�������ʱ��ֻ���۳��г������������ʣ���ʳ�����ڱ����ڶ�������������
�ٵ�ÿ���ʳ����ȫ���۳�ʱ����x��ȡֵ��Χ��
����ÿ���õ�����y����Ԫ�������ۼ۸�x�ĺ�����ϵʽ��
��3���ڣ�2���������£���xΪ����ʱ��y�����ֵ��������������
���𰸡���1��q����x+14������2��x��10����2����2��x��4����y��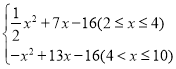 ����3��x��
����3��x��![]() ʱȡ���ֵ���������
ʱȡ���ֵ���������![]() ��Ԫ��
��Ԫ��
��������
��1�����ݱ������ݣ���q��x�ĺ�����ϵʽΪ��q��kx+b������ϵ����������ã�
��2���ٸ������⣬p��q�����㼴�����x��ȡֵ��Χ��
�ڸ�����������=������![]() ���ۼ�-���ۣ����г�����ÿ���õ�����
���ۼ�-���ۣ����г�����ÿ���õ�����![]() ����Ԫ�������ۼ۸�
����Ԫ�������ۼ۸�![]() �ĺ�����ϵ��
�ĺ�����ϵ��
��3�����ݣ�2���е�������������ۼ���.
��1���ɱ�������ݣ���q��x�ĺ�����ϵʽΪ��q��kx+b
���ݱ�������ݵ�![]() �����
�����![]() ��
��
��q��x�ĺ�����ϵʽΪ��q����x+14������2��x��10
��2���ٵ�ÿ��İ��Ʒʳ����ȫ���۳�ʱ����p��q
��![]() x+8�ܩ�x+14�����x��4
x+8�ܩ�x+14�����x��4
��2��x��10�����Դ�ʱ2��x��4
���ɢٿ�֪����2��x��4ʱ��
y����x��2��p����x��2����![]() x+8����
x+8����![]() x2+7x��16
x2+7x��16
��4��x��10ʱ��y����x��2��q��2��p��q��
����x��2������x+14����2[![]() x+8������x+14��]
x+8������x+14��]
����x2+13x��16
����y��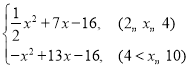
��3����2��x��4ʱ��
y��![]() x2+7x��16�ĶԳ���Ϊx��
x2+7x��16�ĶԳ���Ϊx��![]() ����7
����7
�൱2��x��4ʱ����x�����������
��x��4ʱ�����ֵ��y��20
��4��x��10ʱ
y����x2+13x��16������x��![]() ��2+
��2+![]() ��
��
�ߩ�1��0��![]() ��4
��4
��x��![]() ʱȡ���ֵ
ʱȡ���ֵ
����ʱy���������![]() ��Ԫ��
��Ԫ��