题目内容
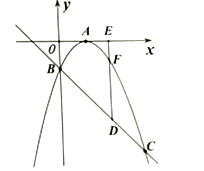
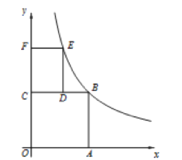
【题目】如图，正方形OABC的边OA，OC在坐标轴上，矩形CDEF的边CD在CB上，且5CD=3CB，边CF在轴上，且CF=2OC-3，反比例函数y=
(k>0)的图象经过点B,E，则点E的坐标是____
【答案】
【解析】
设正方形OABC的边0A=a，可知OA=OC=AB=CB=a，所以点B的坐标为(aa)，推出反比例函数解析式的k=a
，再由CF=2OC-3，可知CF=2a-3，推出点的坐标为(
,3a-3)，根据5CD=3CB，可求出点E的坐标
由题意可设：正方形OABC的边OA=a
∴OA= OC=AB= CB
∴点B的坐标为(a,a)，即k=a
CF=2OC-3
∴CF=2a-3
∵OF=OC+CF=a+2a-3=3a-3
∴点E的纵坐标为3a-3
将3a-3代入反比例函数解析式y=
中,可得点E的横坐标为
∵四边形CDEF为矩形,
∴CD=EF=
5CD=3CB
=3a,可求得:a=
将a=,代入点E的坐标为( ,3a-3),
可得:E的坐标为
故答案为：
练习册系列答案
相关题目
