Question

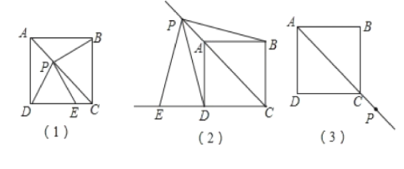
【题目】已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且随着点P的运动而运动，PE=PD总成立。

(1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明)；

(2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立，请给出证明；如果不成立，请说明理由；

(3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)

Answer 1

【答案】（1）①PE=PB，②PE⊥PB；（2）成立，理由见解析（3）①PE=PB，②PE⊥PB.

【解析】

（1）根据正方形的性质和全等三角形的判定定理可证△PDC△PBC，推出PB=PD=PE，∠PDE=180°∠PBC=∠PED，求出∠PEC+∠PBC=180°，求出∠EPB的度数即可

（2）证明方法同（1），可得PE=PB，PE⊥PB

（3）证明方法同（1），可得PE=PB，PE⊥PB

(1)①PE=PB，②PE⊥PB.

(2)(1)中的结论成立。

①∵四边形ABCD是正方形，AC为对角线，

∴CD=CB，∠ACD=∠ACB，

又PC=PC，

∴△PDC≌△PBC，

∴PD=PB，

∵PE=PD，

∴PE=PB，

②：由①,得△PDC≌△PBC，

∴∠PDC=∠PBC.

又∵PE=PD，

∴∠PDE=∠PED.

∴∠PDE+∠PDC=∠PEC+∠PBC=180°，

∴∠EPB=360°(∠PEC+∠PBC+∠DCB)=90°，

∴PE⊥PB.

(3)如图所示：

结论：①PE=PB，②PE⊥PB.