题目内容
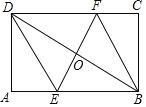
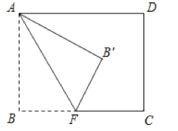
【题目】如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠。当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为___.
【答案】2![]() 或93
或93![]() .
.
【解析】
分两种情况考虑:B′在横对称轴上与B′在竖对称轴上,分别求出BF的长即可.
当B′在横对称轴上,此时AE=EB=3,如图1所示,
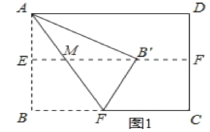
由折叠可得△ABF≌△AB′F
∴∠AFB=∠AFB′,AB=AB′=6,BF=B′F,
∴∠B′MF=∠B′FM,
∴B′M=B′F,
∵EB′∥BF,且E为AB中点,
∴M为AF中点,即EM为中位线,∠B′MF=∠MFB,
∴EM=![]() BF,
BF,
设BF=x,则有B′M=B′F=BF=x,EM=![]() x,即EB′=
x,即EB′=![]() x,
x,
在Rt△AEB′中,根据勾股定理得:3![]() +(
+(![]() x)
x) ![]() =6
=6![]() ,
,
解得:x=2![]() ,即BF=2
,即BF=2![]() ;
;
当B′在竖对称轴上时,此时AM=MD=BN=CN=4,如图2所示:

设BF=x,B′N=y,则有FN=4x,
在Rt△FNB′中,根据勾股定理得:y![]() +(4x)
+(4x) ![]() =x
=x![]() ,
,
∵∠AB′F=90°,
∴∠AB′M+∠NB′F=90°,
∵∠B′FN+∠NB′F=90°,
∴∠B′FN=∠AB′M,
∵∠AMB′=∠B′NF=90°,
∴△AMB′∽△B′NF,
∴![]() ,即
,即![]() ,
,
∴y=![]() x,
x,
∴(![]() x)
x) ![]() +(4x)
+(4x) ![]() =x
=x![]() ,
,
解得x![]() =9+3
=9+3![]() ,x
,x![]() =93
=93![]() ,
,
∵9+3![]() >4,舍去,
>4,舍去,
∴x=93![]()
所以BF的长为2![]() 或93
或93![]() ,
,
故答案为:2![]() 或93
或93![]() .
.

【题目】某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下:(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
+15 | -8 | +6 | +12 | -4 | +5 | -10 |
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.1升,问共耗油多少升?