题目内容
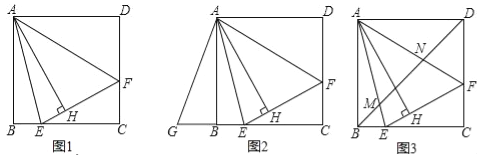
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
【答案】(1)①详见解析;②6;(2)MN2=ND2+BM2,,理由见解析.
【解析】
试题分析:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG,接下来在证明∠GAE=∠FAE,然后依据SAS证明△GAE≌△FAE即可;②由全等三角形的性质可知:AB=AH,GE=EF=5.设正方形的边长为x,在Rt△EFC中,依据勾股定理列方程求解即可;(2)将△ABM逆时针旋转90°得△ADM′.在△NM′D中依据勾股定理可证明NM′2=ND2+DM′2,接下来证明△AMN≌△ANM′,于的得到MN=NM′,最后再由BM=DM′证明即可.
试题解析:(1)①由旋转的性质可知:AF=AG,∠DAF=∠BAG.
∵四边形ABCD为正方形,
∴∠BAD=90°.
又∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠FAE.
在△GAE和△FAE中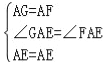 ,
,
∴△GAE≌△FAE.
②∵△GAE≌△FAE,AB⊥GE,AH⊥EF,
∴AB=AH,GE=EF=5.
设正方形的边长为x,则EC=x﹣2,FC=x﹣3.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,即(x﹣2)2+(x﹣3)2=25.
解得:x=6.
∴AB=6.
∴AH=6.
(3)如图所示:将△ABM逆时针旋转90°得△ADM′.
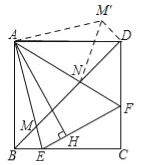
∵四边形ABCD为正方形,
∴∠ABD=∠ADB=45°.
由旋转的性质可知:∠ABM=∠ADM′=45°,BE=DM′.
∴∠NDM′=90°.
∴NM′2=ND2+DM′2.
∵∠EAM′=90°,∠EAF=45°,
∴∠EAF=∠FAM′=45°.
在△AMN和△ANM′中,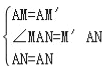 ,
,
∴△AMN≌△ANM′.
∴MN=NM′.
又∵BM=DM′,
∴MN2=ND2+BM2.

 寒假学与练系列答案
寒假学与练系列答案