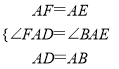题目内容
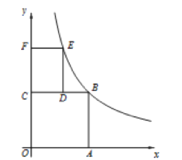
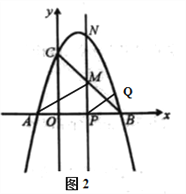
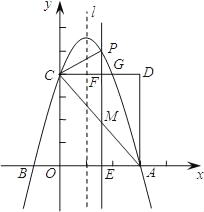
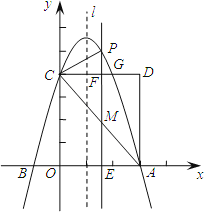
【题目】如图，抛物线y=ax2﹣2ax+c（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．
（1）求抛物线的解析式；
（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；
（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由．
【答案】（1）抛物线的解析式为y=﹣
x2+
x+4；（2）PM=﹣m2+4m（0＜m＜3）；（3）存在这样的点P使△PFC与△AEM相似，此时m的值为
或1，△PCM为直角三角形或等腰三角形．
【解析】试题分析：（1）将A（3，0），C（0，4）代入y=ax2-2ax+c，运用待定系数法即可求出抛物线的解析式；
（2）先根据A、C的坐标，用待定系数法求出直线AC的解析式，进而根据抛物线和直线AC的解析式分别表示出点P、点M的坐标，即可得到PM的长；
（3）由于∠PFC和∠AEM都是直角，F和E对应，则若以P、C、F为顶点的三角形和△AEM相似时，分两种情况进行讨论：①△PFC∽△AEM，②△CFP∽△AEM；可分别用含m的代数式表示出AE、EM、CF、PF的长，根据相似三角形对应边的比相等列出比例式，求出m的值．
试题解析：（1）∵抛物线y=ax2-2ax+c（a≠0）经过点A（3，0），点C（0，4），
∴
，
解得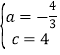
．
∴抛物线的解析式为y=-x2+x+4；
（2）设直线AC的解析式为y=kx+b，
∵A（3，0），点C（0，4），
∴
，
解得
．
∴直线AC的解析式为y=-x+4．
∵点M的横坐标为m，点M在AC上，
∴M点的坐标为（m，-m+4），
∵点P的横坐标为m，点P在抛物线y=-x2+x+4上，
∴点P的坐标为（m，-m2+m+4），
∴PM=PE-ME=（-m2+m+4）-（-m+4）=-m2+4m，
即PM=-m2+4m（0＜m＜3）；
（3）在（2）的条件下，连结PC，在CD上方的抛物线部分存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似．理由如下：由题意，可得AE=3-m，EM=-m+4，CF=m，若以P、C、F为顶点的三角形和△AEM相似，情况：
①P点在CD上方，则PF=-m2+m+4-4=-m2+m．
若△PFC∽△AEM，则PF：AE=FC：EM，
即（-m2+m）：（3-m）=m：（-m+4），
∵m≠0且m≠3，
∴m=；
②若△CFP∽△AEM，则CF：AE=PF：EM，
即m：（3-m）=（-m2+m）：（-m+4），
∵m≠0且m≠3，
∴m=1．
综上所述，存在这样的点P使△PFC与△AEM相似．此时m的值为或1．
