题目内容
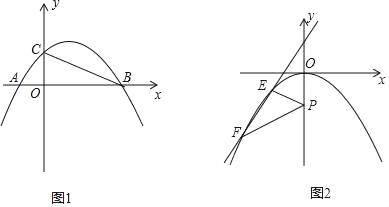
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒
交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
【答案】y=![]() x2﹣
x2﹣![]() x+3; (2,1).
x+3; (2,1).
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据锐角三角函数,可得AE与NE的关系,根据路程与速度,可得点M在整个运动中所用的时间为DE+EN,根据两点之间线段最短,可得当D′、E、N三点共线时,DE+EN最小,根据矩形的判定与性质,可得ND′=OC=3,ON=D′C=DC,根据抛物线与x轴的交点可得OD的长,再求ON的长,可得答案.
解:(1)把A(0,3),C(3,0)代入![]() ,
,
得 ,解得
,解得 .
.
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+3,
x+3,
故答案为y=![]() x2﹣
x2﹣![]() x+3;
x+3;
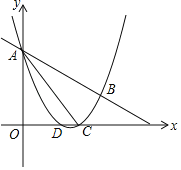
(2)∵A(0,3),C(3,0),
∴OA=OC=3,
∴△AOC是等腰直角三角形,
∴∠OAC=45°,
过点E作EN⊥y轴于N,如图,
在Rt△ANE中,EN=AEsin45°=![]() AE,即AE=
AE,即AE=![]() EN,
EN,
∴点M在整个运动中所用的时间为![]() =DE+EN,
=DE+EN,
作点D关于AC的对称点D′,连接D′E,
则有D′E=DE,D′C=DC,∠D′CA=∠DCA=45°,
∴∠D′CD=90°,DE+EN=D′E+EN,
根据两点之间线段最短可得:当D′、E、N三点共线时,DE+EN=D′E+EN最小,
此时,∵∠D′CD=∠D′NO=∠NOC=90°,
∴四边形OCD′N是矩形,
∴ND′=OC=3,ON=D′C=DC.
对于y=![]() x2﹣
x2﹣![]() x+3,当y=0时,有
x+3,当y=0时,有![]() x2﹣
x2﹣![]() x+3=0,
x+3=0,
解得:x1=2,x2=3.
∴D(2,0),OD=2,
∴ON=DC=OC﹣OD=3﹣2=1,
∴点E的坐标为(2,1),
故答案为(2,1).


 期末集结号系列答案
期末集结号系列答案【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
x | … | ﹣1 | 0 | 3 | … |
y | … | 0 |
| 0 | … |
(1)求抛物线的解析式;
(2)抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥![]() S△BOC,求xQ的取值范围;
S△BOC,求xQ的取值范围;
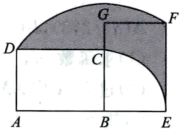
(3)如图2,平移此抛物线使其顶点为坐标原点,P(0,﹣1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.