题目内容
【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
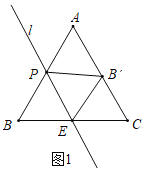
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
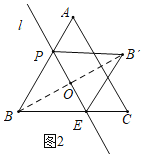
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
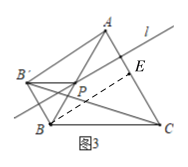
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
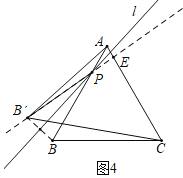
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

【答案】(1)4;(2)5![]() ;(3)面积不变,S△ACB’=
;(3)面积不变,S△ACB’=![]() ;(4)24+4
;(4)24+4![]()
【解析】
(1)证明△APB′是等边三角形即可解决问题;
(2)如图2中,设直线l交BC于点E,连接B B′交PE于O,证明△PEB是等边三角形,求出OB即可解决问题;
(3)如图3中,结论:面积不变,证明B B′//AC即可;
(4)如图4中,当PB′⊥AC时,△ACB′的面积最大,设直线PB′交AC于点E,求出B′E即可解决问题.
(1)如图1,∵△ABC为等边三角形,
∴∠A=60°,AB=BC=CA=8,
∵PB=4,
∴PB′=PB=PA=4,
∵∠A=60°,
∴△APB′是等边三角形,
∴AB′=AP=4,
故答案为:4;
(2)如图2,设直线l交BC于点E,连接B B′交PE于O,
∵PE∥AC,
∴∠BPE=∠A=60°,∠BEP=∠C=60°,
∴△PEB是等边三角形,
∵PB=5,B、B′关于PE对称,
∴BB′⊥PE,BB′=2OB,
∴OB=PB·sin60°=![]() ,
,
∴BB′=5![]() ,
,
故答案为:5![]() ;
;
(3)如图3,结论:面积不变.
过点B作BE⊥AC于E,
则有BE=AB·sin60°=![]() ,
,
∴S△ABC=![]() =16
=16![]() ,
,
∵B、B′关于直线l对称,
∴BB′⊥直线l,
∵直线l⊥AC,
∴AC//BB′,
∴S△ACB’=S△ABC=16![]() ;
;
(4)如图4,当B′P⊥AC时,△ACB′的面积最大,
设直线PB′交AC于E,
在Rt△APE中,PA=2,∠PAE=60°,
∴PE=PA·sin60°=![]() ,
,
∴B′E=B′P+PE=6+![]() ,
,
∴S△ACB最大值=![]() ×(6+
×(6+![]() )×8=24+4
)×8=24+4![]() .
.

【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.





