题目内容
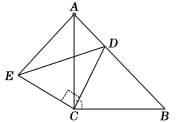
【题目】如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF,连接AF,BF,DE,CE,分别交于H,G.求证: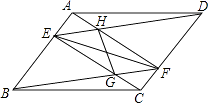
(1)EF与GH互相平分;
(2)在不添加任何辅助线和字母的条件下,请直接写出图中所有的全等的三角形.
【答案】
(1)解:证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴四边形AECF是平行四边形.
∴AF∥CE,
∵AE=CF,AB∥CD,AB=CD,
∴BE∥DF,BE=DF,
∴四边形BFDE是平行四边形,
∴BF∥DE,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分;
(2)解:图中所有的全等的三角形有:△ADE≌△CFB;△AHD≌△BGC;△ABF≌△CDE;△AEH≌△CFG;△EHG≌△FGE.
【解析】(1)要证EF与GH互相平分,需证明四边形EGFH是平行四边形,就需要证明四边形AECF是平行四边形和四边形BFDE是平行四边形,由已知已证得。
(2)由已知及(1)的证明过程和结论,易写出图中的所有的全等三角形。
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目