题目内容
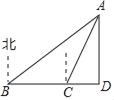
【题目】如图，一艘轮船航行到B处时，测得小岛A在船的北偏东60°的方向上，轮船从B处继续向正东方向航行100海里到达C处时，测得小岛A在船的北偏东30°的方向上，AD⊥BC于点D，求AD的长．
【答案】50
海里.
【解析】
先根据已知和三角形的外角得出△ABC是等腰三角形，得出BC=AC=100海里，在Rt△ACD中，根据直角三角形中30°的角所对的直角边为斜边的一半，求出CD的长，再利用勾股定理求得AD的长．
∵∠ABD＝30°，∠ACD＝60°．
∵∠ACD＝∠ABD+∠CAB
∴∠CAB＝∠ABD=30°，
∴BC＝AC＝100（海里）．
在Rt△ACD中，∠ACD＝60°,∠CAD=30°，
∴CD＝
AC=50（海里）．
∴AD＝
＝
（海里）．
练习册系列答案
相关题目
