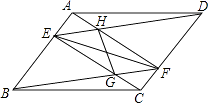
题目内容
【题目】数学课上张老师将课本![]() 页第
页第![]() 题进行了改编,图形不变.请你完成下面问题.
题进行了改编,图形不变.请你完成下面问题.
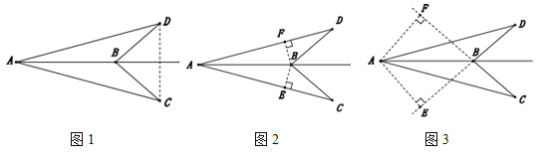
![]() 如图,
如图,![]() .求证:
.求证:![]()
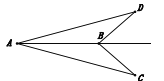
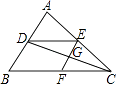
![]() 如图,
如图,![]() .求证:
.求证:![]()
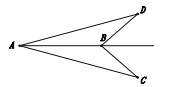
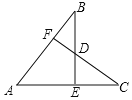
![]() 如图,
如图,![]() 求证:
求证:![]()
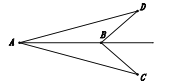
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)连接CD.根据等边对等角,得到∠BCD=∠BDC,进而得到∠ACD=∠ADC.根据等角对等边得到AC=AD.由SSS即可得到结论;
(2)过点B分别作BE⊥AC,BF⊥AD,垂足分别为E,F.根据角平分线的性质得到BE=BF.再由HL证明Rt△BCERt△BDF,根据全等三角形对应角相等得到∠C=∠D,进而由AAS即可证明△ABC△ABD;
(3)过点A分别作AE⊥BD,AF⊥BC,垂足分别为E,F.先证明点A在∠EBF的平分线上,由角平分线的性质即可得到AE=AF.由HL证明Rt△AED≌Rt△AFC,由全等三角形对应角相等得到∠C=∠D.根据AAS即可证明△ABC≌△ABD.
(1)连接CD.
∵BC=BD,∴∠BCD=∠BDC.
∵∠ACB==∠ADB,∴∠ACB+∠BCD=∠ADB+∠BDC,即∠ACD=∠ADC,∴AC=AD.
在△ABC和△ABD中,∵AC=AD,BC=BD,AB=AB,∴△ABC≌△ABD;
(2)过点B分别作BE⊥AC,BF⊥AD,垂足分别为E,F,∴∠BEC=∠BFD=90°.
∵∠CAB=∠DAB,即点B在∠CAD的平分线上,BE⊥AC,BF⊥AD,垂足分别为E,F,∴BE=BF.
在Rt△BCE和Rt△BDF中,∵BC=BD,BE=BF,∴Rt△BCE≌Rt△BDF,∴∠C=∠D.
在△ABC和△ABD中,∵∠C=∠D,∠CAB=∠DAB,AB=AB,∴△ABC≌△ABD;
(3)如图3,过点A分别作AE⊥BD,AF⊥BC,垂足分别为E,F,∴∠AED=∠AFC=90°.
∵∠ABC+∠ABF=∠ABD+∠ABE=180°,∠ABC=∠ABD,∴∠ABF=∠ABE,即点A在∠EBF的平分线上.
∵AE⊥BD,AF⊥BC,垂足分别为E,F,∴AE=AF.
在Rt△AED和Rt△AFC中,∵AD=AC,AE=AF,∴Rt△AED≌Rt△AFC,∴∠C=∠D.
在△ABC和△ABD中,∵∠C=∠D,∠ABC=∠ABD,AB=AB,∴△ABC≌△ABD.