题目内容
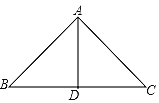
【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.

【答案】(1)65°(2)证明见解析
【解析】
(1)由题意可得∠EAD=![]() ∠BAC=25°,再根据∠AED=90°,利用直角三角形两锐角互余即可求得答案;
∠BAC=25°,再根据∠AED=90°,利用直角三角形两锐角互余即可求得答案;
(2)由于DE⊥AB,易得∠AED=90°=∠ACB,而AD平分∠BAC,易知∠DAE=∠DAC,又因为AD=AD,利用AAS可证△AED≌△ACD,那么AE=AC,DE=DC,根据线段垂直平分线的判定定理即可得证.
(1)∵AD平分∠BAC,∠BAC=50°,
∴∠EAD=![]() ∠BAC=25°,
∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-∠EAD=90°-25°=65°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又AD平分∠BAC,
∴∠DAE=∠DAC,
又∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,DE=DC
∴点A在线段CE的垂直平分线上,点D在线段CE的垂直平分线上,
∴直线AD是线段CE的垂直平分线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目