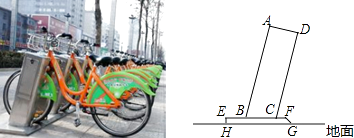��Ŀ����
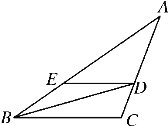
����Ŀ����֪����ͼ������E��������ABCD��BC���ϣ�BF��AE�ڵ�F��DG��AE�ڵ�G����֪��ADG�ա�BAF.����Ҫ��֤����

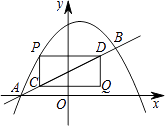
��չ����ͼ������B��C����MAN�ı�AM��AN�ϣ���E, F����MAN�ڲ�������AD�ϣ���1����2�ֱ�����ABE����CAF����ǣ���֪AB=AC,��1=��2=��BAC.��֤����ABE�ա�CAF.
Ӧ�ã���ͼ�����ڵ���������ABC�У�AB=AC��AB��BC����D�ڱ�B�ϣ�CD=2BD.��E, F���߶�AD�ϣ���1=��2=��BAC������ABC�����Ϊ9������ABE����CDF�����֮��Ϊ_________.
���𰸡���չ��֤����������Ӧ�ã�6
��������
��չ��֤������ͼ��
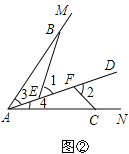
�ߡ�1=��2�����BEA=��AFC��
�ߡ�1=��ABE+��3����3+��4=��BAC����1=��BAC��
���BAC=��ABE+��3�����4=��ABE��
�ߡ�AEB=��AFC����ABE=��4��AB=AC��
���ABE�ա�CAF��AAS����
Ӧ�ã�6��
��չ��������1=��2=��BAC������������������ʵó���4=��ABE���Ӷ�����AAS֤����ABE�ա�CAF��
Ӧ�ã����ȸ�����ABD����ADC�ȸߣ��ױ߱�ֵΪ��1��2���ó���ABD����ADC�����Ϊ��1��2����֤����ABE�ա�CAF�����ɵó���ABE����CDF�����֮��Ϊ��ADC������ó��𰸼��ɣ�
��ͼ��
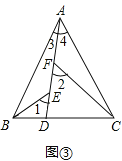
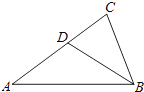
���ڵ���������ABC�У�AB=AC��CD=2BD��
���ABD����ADC�ȸߣ��ױ߱�ֵΪ��1��2��
���ABD����ADC�������1��2��
�ߡ�ABC�����Ϊ9�����ABD����ADC����ֱ�Ϊ��3��6��
�ߡ�1=��2�����BEA=��AFC��
�ߡ�1=��ABE+��3����3+��4=��BAC����1=��BAC��
���BAC=��ABE+��3�����4=��ABE��
�ߡ�AEB=��AFC����ABE=��4��AB=AC�����ABE�ա�CAF��AAS����
���ABE����CAF�����ȣ����ABE����CDF�����֮��Ϊ��ADC�������
���ABE����CDF�����֮��Ϊ6��

 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д�