题目内容
【题目】如图，在△ABC中，D为AC边上一点，∠DBC=∠A．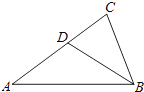
（1）求证：△BCD∽△ACB；
（2）如果BC= 
，AC=3，求CD的长．
【答案】
（1）
证明：∵∠DBC=∠A，∠C=∠C，
∴△BCD∽△ACB；
（2）
解：∵△BCD∽△ACB，
∴ 
，
∴ 
= 
，
∴CD=2．
【解析】（1）根据相似三角形的判定得出即可；（2）根据相似得出比例式，代入求出即可．
【考点精析】利用相似三角形的性质和相似三角形的判定对题目进行判断即可得到答案，需要熟知对应角相等，对应边成比例的两个三角形叫做相似三角形；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】2015年4月30日，苏州吴江蚕种全部发放完毕，共计发放蚕种6460张（每张上的蚕卵有200粒左右），涉及6个镇，各镇随即开始孵化蚕种，小李所记录的蚕种孵化情况如表所示，则可以估计蚕种孵化成功的概率为（ ）
累计蚕种孵化总数/粒 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
孵化成功数/粒 | 181 | 362 | 541 | 718 | 905 | 1077 | 1263 |
A.0.95
B.0.9
C.0.85
D.0.8
