题目内容
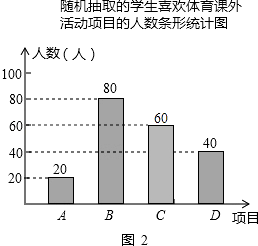
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
【答案】
(1)200
(2)
解:C项目对应人数为:200﹣20﹣80﹣40=60(人);
补充如图.
(3)
解:列表如下:
甲 | 乙 | 丙 | 丁 | |
甲 | ﹨ | (乙,甲) | (丙,甲) | (丁,甲) |
乙 | (甲,乙) | ﹨ | (丙,乙) | (丁,乙) |
丙 | (甲,丙) | (乙,丙) | ﹨ | (丁,丙) |
丁 | (甲,丁) | (乙,丁) | (丙,丁) | ﹨ |
∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,
∴P(选中甲、乙)= ![]() =
= ![]() .
.
【解析】解:(1)根据题意得:这次被调查的学生共有20÷ ![]() =200(人).
=200(人).
故答案为:200;
(1)由题意可知这次被调查的学生共有20÷ ![]() =200(人);(2)首先求得C项目对应人数为:200﹣20﹣80﹣40=60(人),继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.
=200(人);(2)首先求得C项目对应人数为:200﹣20﹣80﹣40=60(人),继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.

 阅读快车系列答案
阅读快车系列答案【题目】2015年4月30日,苏州吴江蚕种全部发放完毕,共计发放蚕种6460张(每张上的蚕卵有200粒左右),涉及6个镇,各镇随即开始孵化蚕种,小李所记录的蚕种孵化情况如表所示,则可以估计蚕种孵化成功的概率为( )
累计蚕种孵化总数/粒 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
孵化成功数/粒 | 181 | 362 | 541 | 718 | 905 | 1077 | 1263 |
A.0.95
B.0.9
C.0.85
D.0.8