Question

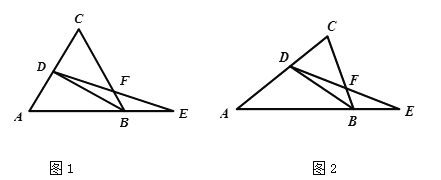
【题目】在△ABC中，AB＝AC，∠ABC的平分线交AC于点D，在AB的延长线上截取BE，使BE＝CD，连接DE交BC于点F．

（1）如图1，当∠CAB＝60°时，若AB＝2，求DE的长度；

（2）如图2，当∠CAB≠60°时，求证：BE＝2BF．

Answer 1

【答案】（1）；（2）答案见解析．

【解析】试题分析：（1）如图1中，作DH⊥AB于H．在Rt△DEH中，求出DH、EH，利用勾股定理即可解决问题；

（2）如图2中，作DH∥AB交BC于H，连接EH．只要证明四边形DBEH是平行四边形，再证明BH=BE，即可解决问题．

试题解析：解：（1）如图1中，作DH⊥AB于H．

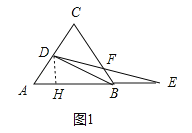
∵AC=AB，∠CAB=60°，∴△ABC是等边三角形，∴AB=BC=AC=2，∠A=60°．∵BD平分∠ABC，∴AD=DC=1．在Rt△ADH中，∵∠ADH=30°，AD=1，∴AH=，DH=．∵BE=CD=1，∴EH=BH+BE=．在Rt△DHE中，DE===．

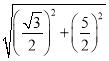（2）如图2中，作DH∥AB交BC于H，连接EH．

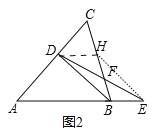
∵AB=AC，∴∠C=∠ABC．∵DH∥AB，∴∠DHC=∠ABC=∠C，∴DH=DC．∵DC=BE，∴四边形DBEH是平行四边形，∴FH=FB，BD∥EH，∴∠BHE=∠DBH，∠DBA=∠BEH．∵∠DBA=∠DBC，∴∠BHE=∠BEH，∴BH=BE，∴BE=2BF．