题目内容
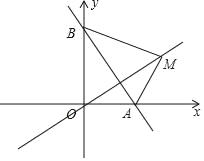
【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+![]() =0.
=0.
(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
【答案】(1)y=﹣2x+4;(2)m=1.
【解析】
(1)根据非负数的性质可求得p、q,可求得A、B坐标,利用待定系数法可求得直线AB的解析式;
(2)根据A、B坐标,可求出AB及AB中点的C坐标,设M坐标为(x,mx),则MC=![]() AB,且M点在线段AB的垂直平分线上,可求得垂直平分线的方程,则可求得M的值.
AB,且M点在线段AB的垂直平分线上,可求得垂直平分线的方程,则可求得M的值.
解:(1)根据题意可得:p﹣2=0,解得 p=2,
根据题意可得:q﹣4=0 解得:q=4,
设直线AB的解析式为y=kx+4( k≠0)
将A(2,0)代入得
2k+4=0
k=﹣2
∴AB的解析式为y=﹣2x+4;
(2)过M点作MH⊥y轴于H,过M点作MN⊥x轴于N
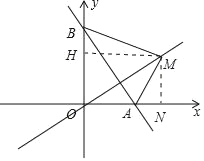
∴∠BHM=∠MNA=90°
∵∠BON=90°
∴∠HMN=90°
∴∠HMA+∠AMN=90°
∵△ABM是以AB为底的等腰直角三角形
∴MB=MA,∠BMA=90°
∴∠HMA+∠BMH=90°
∴∠AMN=∠BMH
∴△BHM≌△AMN
∴MH=MN,
设M的坐标为(x,y)
则x=y
∴mx=x
∴m=1.

【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
(1)求![]() 、
、![]() 两种型号的空调的销售价;
两种型号的空调的销售价;
(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.