题目内容
【题目】如图,从楼AB的A处测得对面楼CD的顶部C的仰角为37°,底部D的俯角为45°,两楼的水平距离BD为24 m,那么楼CD的高度约为________ m.(结果精确到1 m,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
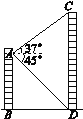
【答案】42
【解析】
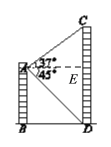
如下图,过点A作AE⊥CD于E,结合已知条件易得四边形ABDE是矩形,由此可得AE=AD=24米,这样在Rt△ACE和Rt△AED中,结合已知条件解得CE和DE的长即可得到楼高CD的长度了.
过点A作AE⊥CD于点E,
∴∠AEC=∠AED=90°,
∵∠ABD=∠BDC=90°,
∴四边形ABDE是矩形,
∴AE=BD=24m,
∵在Rt△ACE中,BD=AE=24 m,∠CAE=37°,
∴CE=AE·tan37°≈24×0.75=18(m).
∵在Rt△AED中,∠EAD=45°,
∴DE=AE=24 m,
∴CD=CE+DE≈18+24=42 (m).
故楼CD的高度大约为42 m.
故答案为:42.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目