题目内容
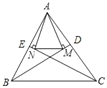
【题目】如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC的周长为30,BC=12.则MN的长是( )
A. 15B. 9C. 6D. 3
【答案】D
【解析】
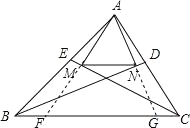
延长AM、AN分别交BC于点F、G,根据BN为∠ABC的角平分线,AN⊥BN得出∠BAN=∠G,故△ABG为等腰三角形,所以BN也为等腰三角形的中线,即AN=GN.同理AM=MF,根据三角形中位线定理即可得出结论.
∵△ABC的周长为30,BC=12.
∴AB+AC=30﹣BC=18.
延长AN、AM分别交BC于点F、G.如图所示:
∵BN为∠ABC的角平分线,
∴∠CBN=∠ABN,
∵BN⊥AG,
∴∠ABN+∠BAN=90°,∠AGB +∠CBN=90°,
∴∠BAN=∠AGB,
∴AB=BG,
∴AN=GN,
同理AC=CF,AM=MF,
∴MN为△AFG的中位线,GF=BG+CF﹣BC,
∴MN=![]() (AB+AC﹣BC)=
(AB+AC﹣BC)=![]() (18﹣12)=3.
(18﹣12)=3.
故选:D.

练习册系列答案
相关题目