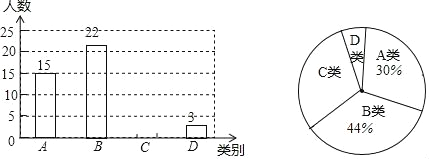
题目内容
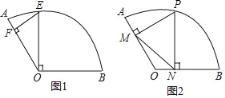
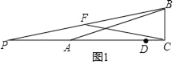
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=2,AC=6,在AC上取一点D,使AD=4,将线段AD绕点A按顺时针方向旋转,点D的对应点是点P,连接BP,取BP的中点F,连接CF,当点P旋转至CA的延长线上时,CF的长是_____,在旋转过程中,CF的最大长度是_____.
【答案】![]() ,
, ![]() +2.
+2.
【解析】
当点P旋转至CA的延长线上时,CP=10,BC=2,利用勾股定理求出BP,再根据直角三角形斜边上的中线等于斜边的一半,可得CF的长;取AB的中点M,连接MF和CM,根据直角三角形斜边上的中线等于斜边的一半,可得CM的长,利用三角形中位线定理,可得FM的长,再根据当且仅当M、F、C三点共线且M在线段CF上时CF最大,即可得到结论.
当点P旋转至CA的延长线上时,如图1.
∵在直角△BCP中,∠BCP=90°,CP=AC+AP=6+4=10,BC=2,
∴BP=![]() ,
,
∵BP的中点是F,
∴CF=![]() BP=
BP=![]() .
.
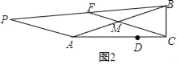
取AB的中点M,连接MF和CM,如图2.
∵在直角△ABC中,∠ACB=90°,AC=6,BC=2,
∴AB![]() =2
=2![]() .
.
∵M为AB中点,
∴CM=![]() AB=
AB=![]() ,
,
∵将线段AD绕点A按顺时针方向旋转,点D的对应点是点P,
∴AP=AD=4,
∵M为AB中点,F为BP中点,
∴FM=![]() AP=2.
AP=2.
当且仅当M、F、C三点共线且M在线段CF上时CF最大,
此时CF=CM+FM=![]() +2.
+2.
故答案为:![]() ,
,![]() +2.
+2.

练习册系列答案
相关题目