ЬтФПФкШн
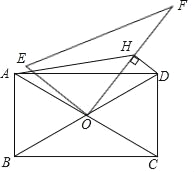
ЁОЬтФПЁПвбжЊдкЩШаЮAOBжаЃЌдВаФНЧЁЯAOBЃН120ЁуЃЌАыОЖOAЃНOBЃН8ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуOзїOEЁЭOBЃЌНЛЛЁABгкЕуEЃЌдйЙ§ЕуEзїEFЁЭOAгкЕуFЃЌЧѓFOЕФГЄЃЌЁЯFEOЕФЖШЪ§ЃЛ
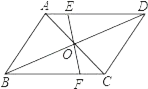
ЃЈ2ЃЉШчЭМ2ЃЌЩшЕуPЮЊЛЁABЩЯЕФЖЏЕуЃЌЙ§ЕуPзїPMЁЭOAгкЕуMЃЌPNЁЭOBгкЕуNЃЌЕуMЃЌNЗжБ№дкАыОЖOAЃЌOBЩЯЃЌСЌНгMNЃЌдђ
ЂйЧѓЕуPдЫЖЏЕФТЗОЖГЄЪЧЖрЩйЃП
ЂкMNЕФГЄЖШЪЧЗёЪЧЖЈжЕЃПШчЙћЪЧЃЌЧыЧѓГіетИіЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЛ
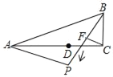
ЃЈ3ЃЉдкЃЈ2ЃЉжаЕФЬѕМўЯТЃЌШєЕуDЪЧЁїPMNЕФЭтаФЃЌжБНгаДГіЕуDдЫЖЏЕФТЗОГЄЃЎ
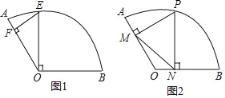
ЁОД№АИЁПЃЈ1ЃЉOFЃН4![]() ЃЌЁЯFEOЃН60ЁуЃЌЃЈ2ЃЉЂйЕуPдЫЖЏЕФТЗОЖГЄЮЊ
ЃЌЁЯFEOЃН60ЁуЃЌЃЈ2ЃЉЂйЕуPдЫЖЏЕФТЗОЖГЄЮЊ![]() ЃЛЂкMNЃН4
ЃЛЂкMNЃН4![]() ЃЌЪЧЖЈжЕЃЛЃЈ3ЃЉЕуDдЫЖЏЕФТЗОГЄЮЊ
ЃЌЪЧЖЈжЕЃЛЃЈ3ЃЉЕуDдЫЖЏЕФТЗОГЄЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіЁЯAOEЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЂйЕБЕуMгыЕуOжиКЯЪБЃЌЁЯPMBЃН30ЁуЃЌЕБЕуNгыЕуOжиКЯЪБЃЌЁЯPNAЃН30ЁуЃЌНјЖјЧѓГіЕуPдЫЖЏТЗОЖЫљЖдЕФдВаФНЧЪЧ120ЁуЉ30ЁуЉ30ЁуЃН60ЁуЃЌзюКѓгУЛЁГЄЙЋЪНМДПЩЕУГіНсТлЃЛ
ЂкЯШХаЖЯГіЕуPЃЌMЃЌOЃЌNЫФЕуОљдкЭЌвЛИідВЃЌМДЁбHЩЯЃЌНјЖјЧѓГіMKЃН2![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіШ§НЧаЮPMNЕФЭтНгдВЕФдВаФЕФдЫЖЏЙьМЃЃЌзюКѓИљОнЛЁГЄЙЋЪНМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЁпOEЁЭOBЃЌ
ЁрЁЯBOEЃН90ЁуЃЌ
ЁпЁЯAOBЃН120ЁуЃЌ
ЁрЁЯAOEЃН30ЁуЃЌ
ЁпEFЁЭOAЃЌ
ЁрЁЯEFOЃН90ЁуЃЌ
дкRtЁїEFOжаЃЌOEЃНOBЃН8ЃЎ
ЁрOFЃНOEcos30ЁуЃН4![]() ЃЌЁЯFEOЃН90ЁуЉ30ЁуЃН60ЁуЃЌ
ЃЌЁЯFEOЃН90ЁуЉ30ЁуЃН60ЁуЃЌ
ЙЪД№АИЮЊЃК4![]() ЃЌ60ЃЛ
ЃЌ60ЃЛ
ЃЈ2ЃЉЂйЕуPдкЛЁABЩЯдЫЖЏЃЌЦфТЗОЖвВЪЧвЛЖЮЛЁЃЌгЩЬтвтПЩжЊЃЌ
ЕБЕуMгыЕуOжиКЯЪБЃЌЁЯPMBЃН30ЁуЃЌ
ЕБЕуNгыЕуOжиКЯЪБЃЌЁЯPNAЃН30ЁуЃЌ
ЁрЕуPдЫЖЏТЗОЖЫљЖдЕФдВаФНЧЪЧ120ЁуЉ30ЁуЉ30ЁуЃН60ЁуЃЌ
ЁрЕуPдЫЖЏЕФТЗОЖГЄЃН![]() ЃЛ
ЃЛ
ЂкЪЧЖЈжЕЃЛ
ШчЭМ1ЃЌСЌНгPOЃЌШЁPOЕФжаЕуHЃЌСЌНгMHЃЌNHЃЌ
ЁпдкRtЁїPMOКЭRtЁїPNOжаЃЌЕуHЪЧаББпPOЕФжаЕуЃЌ
ЁрMHЃНNHЃНPHЃНOHЃН![]() POЃН4ЃЌ
POЃН4ЃЌ
ЁрИљОндВЕФЖЈвхПЩжЊЃЌЕуPЃЌMЃЌOЃЌNЫФЕуОљдкЭЌвЛИідВЃЌМДЁбHЩЯЃЌ
гжЁпЁЯMONЃН120ЁуЃЌЁЯPMOЃНЁЯPNOЃН90ЁуЃЌ
ЁрЁЯMPNЃН60ЁуЃЌЁЯMHNЃН2ЁЯMPNЃН120ЁуЃЌ
Й§ЕуHзїHKЁЭMNЃЌДЙзуЮЊЕуKЃЌ
гЩДЙОЖЖЈРэЕУЃЌMKЃНKNЃН![]() MNЃЌ
MNЃЌ
ЁрдкRtЁїHMKжаЃЌЁЯMHKЃН60ЁуЃЌMHЃН4ЃЌдђMKЃН2![]() ЃЌ
ЃЌ
ЁрMNЃН2MKЃН4![]() ЃЌЪЧЖЈжЕЃЎ
ЃЌЪЧЖЈжЕЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌЕуPЃЌMЃЌOЃЌNЫФЕуЙВдВЃЌ
ЁрHЪЧЁїPMNЕФЭтНгдВЕФдВаФЃЌ
МДЃКЕуHКЭЕуDжиКЯЃЌ
ЁрODЃНPDЃЌ
ЁрЕуDЪЧвдЕуOЮЊдВаФ![]() OPЃН4ЮЊАыОЖЃЌ
OPЃН4ЮЊАыОЖЃЌ
ЁпЕуPдЫЖЏТЗОЖЫљЖдЕФдВаФНЧЪЧ120ЁуЉ30ЁуЉ30ЁуЃН60ЁуЃЌ
ЁрЕуDдЫЖЏТЗОЖЫљЖдЕФдВаФНЧЪЧ120ЁуЉ30ЁуЉ30ЁуЃН60ЁуЃЌ
ЁрЕуDдЫЖЏЕФТЗОГЄЮЊ![]() ЃЎ
ЃЎ

 ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ
ЛЦИдаЁзДдЊТњЗжГхДЬЮЂВтбщЯЕСаД№АИ аТИЈНЬЕМбЇЯЕСаД№АИ
аТИЈНЬЕМбЇЯЕСаД№АИ бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ
бєЙтЭЌбЇвЛЯпУћЪІШЋгХКУОэЯЕСаД№АИ