题目内容
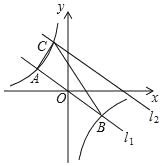
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
【答案】(1)y= ![]() ;(2)y=﹣
;(2)y=﹣![]() x+
x+![]() ;
;
【解析】
(1)根据已知条件y=﹣![]() x经过点A,且A点的纵坐标是2,求得点A的坐标,再把点A的坐标代入y=
x经过点A,且A点的纵坐标是2,求得点A的坐标,再把点A的坐标代入y=![]() 求得k值,即可求得反比例函数的解析式;(2)如图,过F作FD⊥AB于D,过A作AE⊥x轴,则∠FDO=∠OEA=90°,结合A(﹣4,2)可得AE=2,OE=4,AO=2
求得k值,即可求得反比例函数的解析式;(2)如图,过F作FD⊥AB于D,过A作AE⊥x轴,则∠FDO=∠OEA=90°,结合A(﹣4,2)可得AE=2,OE=4,AO=2![]() ,由此可得AB=2AO=4
,由此可得AB=2AO=4![]() ,根据三角形的面积公式求得DF==3
,根据三角形的面积公式求得DF==3![]() ,再证明△AOE∽△OFD,根据相似三角形的性质求得OF=
,再证明△AOE∽△OFD,根据相似三角形的性质求得OF=![]() ,即可求得点F的坐标,设平移后的直线l2的函数表达式为y=﹣
,即可求得点F的坐标,设平移后的直线l2的函数表达式为y=﹣![]() x+b,把点F的坐标代入即可求得b值,从而求得直线l2的函数表达式.
x+b,把点F的坐标代入即可求得b值,从而求得直线l2的函数表达式.
(1)直线l1:y=﹣![]() x经过点A,且A点的纵坐标是2,
x经过点A,且A点的纵坐标是2,
∴令y=2,则x=﹣4,
即A(﹣4,2),
∵反比例函数y=![]() 的图象经过A点,
的图象经过A点,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为y=﹣![]() ;
;
(2)如图,过F作FD⊥AB于D,过A作AE⊥x轴,则∠FDO=∠OEA=90°,
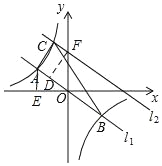
∴AE=2,OE=4,AO=2![]() ,
,
∴AB=2AO=4![]() ,
,
∵直线l1与直线l2平行,△ABC的面积为30,
∴![]() AB×DF=30,即
AB×DF=30,即![]() ×4
×4![]() ×DF=30,
×DF=30,
∴DF=3![]() ,
,
∵∠EOF=90°,
∴∠AOE+∠DOF=90°=∠OFD+∠DOF,
∴∠AOE=∠OFD,
∴△AOE∽△OFD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴FO=![]() ,
,
即F(0,![]() ),
),
设平移后的直线l2的函数表达式为y=﹣![]() x+b,则
x+b,则
![]() =0+b,
=0+b,
∴b=![]() ,
,
∴平移后的直线l2的函数表达式为y=﹣![]() x+
x+![]() .
.

【题目】“发展脐橙产业,加快脱贫的步伐”.某脐橙种植户新鮮采摘了20筐脐橙,以每筐25千克为标准重量,超过或不足干克数分别用正,负数来表示,记录如下:
与标准重量的差值(单位:干克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)与标准重量比较,20筐脐橙总计超过或不足多少千克?
(2)若脐橙毎干克售价6.5元,则出售这20筐脐橙可获得多少元?