题目内容
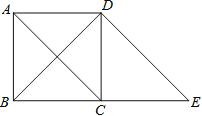
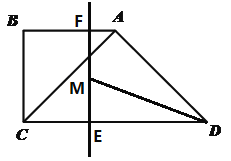
【题目】如图,在矩形ABCD中,EH垂直平分BD,交BD于点M,过BD上一点F作FG∥BE,FG恰好平分∠EFD,FG与EH交于点N.
(1)求证:DEDG=DFBF;
(2)若AB=3,AD=9,求FN的长.
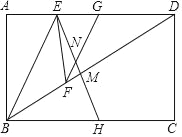
【答案】(1)证明见解析;(2)FN=![]() .
.
【解析】分析:(1)由线段垂直平分线的性质可得BE=DE,根据等边对等角得出∠1=∠2.再证明∠3=∠5,那么△BEF∽△DFG,根据相似三角形对应边成比例可得![]() =
=![]() ,将BE=DE代入即可证明DEDG=DFBF;
,将BE=DE代入即可证明DEDG=DFBF;
(2)设DE=x,则BE=x,在Rt△ABE中根据勾股定理得出32+(9-x)2=x2,解方程求出x=5.在Rt△ABD中,由勾股定理求出BD=![]() =
=![]() ,那么BM=DM=
,那么BM=DM=![]() .再证明BE2=BFDB,求出BF=
.再证明BE2=BFDB,求出BF=![]() =
=![]() ,那么FM=BM-BF=
,那么FM=BM-BF=![]() .再由FN∥BE,得出△MNF∽△MEB,根据相似三角形对应边成比例可得
.再由FN∥BE,得出△MNF∽△MEB,根据相似三角形对应边成比例可得![]() =
=![]() ,即可求出FN=
,即可求出FN=![]() .
.
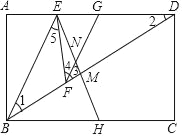
详解:(1)证明:如图.∵EH垂直平分BD,
∴BE=DE,∠1=∠2.
∵FG平分∠EFD,
∴∠3=∠4.
∴FG∥BE,
∴∠4=∠5,
∴∠3=∠5,
∴△BEF∽△DFG,
∴![]() =
=![]() ,
,
∵BE=DE,
∴![]() =
=![]() ,
,
∴DEDG=DFBF;
(2)解:设DE=x,则BE=x,
∵AB=3,AD=9,
∴AE=9﹣x.
在Rt△ABE中,∵∠A=90°,
∴AB2+AE2=BE2,即32+(9﹣x)2=x2,
解得x=
在Rt△ABD中,∵∠A=90°,AB=3,AD=9,
∴BD=![]() =3
=3![]() ,
,
∴BM=DM=![]() .
.
由(1)得![]() =
=![]() ,
,
∵FG∥BE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵BE=DE,
∴BE2=BFDB,
∴BF=![]() =
=![]() =
=![]() ,
,
∴FM=BM﹣BF=![]() ﹣
﹣![]() =
=![]() .
.
∵FN∥BE,
∴△MNF∽△MEB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得FN=![]() .
.

练习册系列答案
相关题目